题目内容
11.计算$\frac{5x+3y}{{x}^{2}-{y}^{2}}$-$\frac{2x}{{x}^{2}-{y}^{2}}$的结果是$\frac{3}{x-y}$.分析 根据同分母分式加减运算法则计算即可,最后要注意将结果化为最简分式.
解答 解:原式=$\frac{5x+3x-2x}{(x+y)(x-y)}$
=$\frac{3(x+y)}{(x+y)(x-y)}$
=$\frac{3}{x-y}$,
故答案为:$\frac{3}{x-y}$.
点评 本题考查了分式的加减,归纳提炼:分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
相关题目
1.一个正方形的面积是10,估计它的边的长度在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
3.函数y=$\frac{\sqrt{x}}{x-1}$中,自变量的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0,且x≠1 |
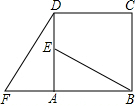 如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13
如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13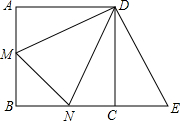 已知正方形ABCD中,M,N分别是AB,BC上的点,∠MDN=45°,延长BC至E,CE=AM,连接DE,MN,求证:NE=MN.
已知正方形ABCD中,M,N分别是AB,BC上的点,∠MDN=45°,延长BC至E,CE=AM,连接DE,MN,求证:NE=MN. 已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.
已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.