题目内容
2.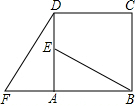 如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13
如图,在正方形ABCD中,E是边AD上一点,将△ABE绕点A按逆时针方向旋转90°到△ADF的位置.已知AF=5,BE=13(1)求DE的长度;
(2)BE与DF是否垂直?说明你的理由.
分析 (1)根据旋转的性质得DF=BE=13,AE=AF=5,再在Rt△ADF中利用勾股定理可计算出AD=12,所以DE=AD-AE=7;
(2)延长BE交DF于H,根据旋转的性质得∠ABE=∠ADF,由于∠ADF+∠F=90°,则∠ABE+∠F=90°,根据三角形内角和定理可计算出∠FHB=90°,于是可判断BH⊥DF.
解答 解:(1)∵△ABE绕点A按逆时针方向旋转90°得到△ADF,
∴DF=BE=13,AE=AF=5,
在Rt△ADF中,∵AF=3,DF=13,
∴AD=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴DE=AD-AE=12-5=7;
(2)BE与DF垂直.理由如下: 延长BE交DF于H,
延长BE交DF于H,
∵△ABE绕点A按逆时针方向旋转90°得到△ADF,
∴∠ABE=∠ADF,
∵∠ADF+∠F=90°,
∴∠ABE+∠F=90°,
∴∠FHB=90°,
∴BH⊥DF.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.若ab<0,$\frac{n}{m}$<0,则一次函数y=$\frac{a}{b}$x+mn一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.下列数学表达式中:①-2<0,②2x+3y>0,③x=2,④x2+2xy+y2,⑤x≠3,⑥x+1>2中,不等式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.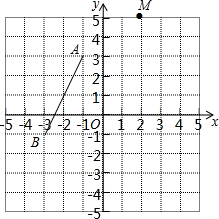 如图,在平面直角坐标系xOy中,将线段AB平移得到线段MN,若点A(-1,3)的对应点为M(2,5),则点B(-3,-1)的对应点N的坐标是( )
如图,在平面直角坐标系xOy中,将线段AB平移得到线段MN,若点A(-1,3)的对应点为M(2,5),则点B(-3,-1)的对应点N的坐标是( )
 如图,在平面直角坐标系xOy中,将线段AB平移得到线段MN,若点A(-1,3)的对应点为M(2,5),则点B(-3,-1)的对应点N的坐标是( )
如图,在平面直角坐标系xOy中,将线段AB平移得到线段MN,若点A(-1,3)的对应点为M(2,5),则点B(-3,-1)的对应点N的坐标是( )| A. | (1,0) | B. | (0,1) | C. | (-6,0) | D. | (0,-6) |
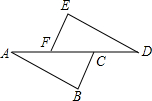 如图,已知BC∥EF,BC=EF,AF=DC,那么AB=DE吗?请说明你的理由.小明的解题过程如下,请你将每一步的理由补充完整.
如图,已知BC∥EF,BC=EF,AF=DC,那么AB=DE吗?请说明你的理由.小明的解题过程如下,请你将每一步的理由补充完整.