题目内容
10.如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.
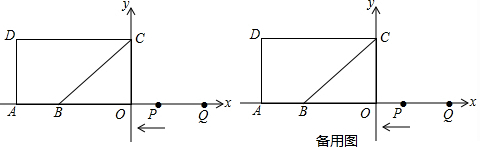
分析 (1)由题意可知△BOC是等腰直角三角形,由此即可解决问题.
(2)如图1中,分两种情形①当点P在点B右侧时,②当点P′在点B左侧时,分别解直角三角形即可.
(3)如图2中,由题意知,若该圆与四边形ABCD的边相切,有三种情况:①当该圆与BC相切于点C时.②当该圆与CD相切于点C时.③当该圆与AD相切时,设P3(8-t,0),设圆心为M,则M($\frac{8-t}{2}$,3),半径r=($\frac{8-t}{2}$)2+32,列出方程即可解决问题.分别求出PQ即可解决问题.
解答 解:(1)∵∠BOC=90°,∠CBO=45°,
∴∠BCO=∠CBO=45°,
∵B(-6,0),
∴OC=OB=6,
∴C(0,6);
(2)如图1中,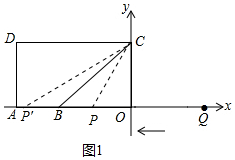
①当点P在点B右侧时,
∵∠BCO=45°,∠BCP=15°,∴∠POC=30°,
∴OP=2$\sqrt{3}$
∴t1=8+2$\sqrt{3}$.
②当点P′在点B左侧时,
∵∠BCO=45°,∠BCP′=15°,∴∠P′CO=60°,
∴OP′=6$\sqrt{3}$,
∴t2=8+6$\sqrt{3}$.
综上所述:t的值为8+2$\sqrt{3}$或8+6$\sqrt{3}$.
(3)如图2中,由题意知,若该圆与四边形ABCD的边相切,有以下三种情况: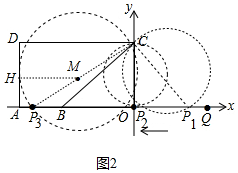
①当该圆与BC相切于点C时,有∠BCP=90°,
从而∠OCP=45°,得到OP1=6,此时P1Q=2,
∴t=2;
②当该圆与CD相切于点C时,有P2C⊥CD,即点P2与点O重合,
此时P2Q=8,
∴t=8;
③当该圆与AD相切时,设P3(8-t,0),设圆心为M,则M($\frac{8-t}{2}$,3),半径r=($\frac{8-t}{2}$)2+32,
作MH⊥AD于点H,则MH=$\frac{8-t}{2}$-(-10)=14-$\frac{t}{2}$,
当MH2=r2时,得(14-$\frac{t}{2}$)2=($\frac{8-t}{2}$)2+32,
解得t=17.1,
∴t的值为2或8或17.1.
点评 本题考查圆综合题、矩形的性质、锐角三角函数,解直角三角形等知识,解题的关键是学会分类讨论,注意不能漏解,学会用方程的思想思考问题,属于中考压轴题.

| A. | 0.28与0.280 | B. | 0.70与0.07 | C. | 5百万与500万 | D. | 1100与1.1×103 |
| A. | 三角形的角平分线 | B. | 三角形的中线 | ||
| C. | 三角形的高 | D. | 以上都不对 |
| A. | 6℃ | B. | 7℃ | C. | 8℃ | D. | 57℃ |
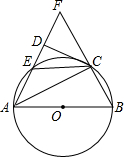 如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,
如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,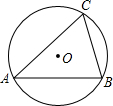 如图,锐角△ABC是⊙O的内接三角形,若AC=17cm,BC=10cm,⊙O的直径是21.25cm,则△ABC的面积是84cm2.
如图,锐角△ABC是⊙O的内接三角形,若AC=17cm,BC=10cm,⊙O的直径是21.25cm,则△ABC的面积是84cm2.
 如图所示的立方体的六个面分别标着连续的整数,则这六个数的和为27或33或39.
如图所示的立方体的六个面分别标着连续的整数,则这六个数的和为27或33或39.