题目内容
17.已知A,B的坐标分别为(2,0),(3,0),若二次函数y=x2+(a-1)x+1的图象与线段AB只有一个交点,则a的取值范围是-$\frac{7}{3}$≤x≤-$\frac{3}{2}$.分析 根据题意,当二次函数顶点在x轴下方或当二次函数的顶点在x轴上时,分情况讨论问题.借助于根的判别式即可解答.
解答 解:(1)顶点在x轴上:$\left\{\begin{array}{l}{2<-\frac{a-1}{2}<3}\\{△=(a-1)^{2}-4=0}\end{array}\right.$,无解
(2)顶点在x轴下方时,因为抛物线过点点(0,1),①$\left\{\begin{array}{l}{4+2(a-1)+1≥0}\\{9+3(a-1)+1≤0}\end{array}\right.$,无解
②$\left\{\begin{array}{l}{4+2(a-1)+1≤0}\\{9+3(a-1)+1≥0}\end{array}\right.$,解得:-$\frac{7}{3}$≤x≤-$\frac{3}{2}$,
所以:-$\frac{7}{3}$≤x≤-$\frac{3}{2}$;
点评 本题涉及二次函数的综合性质,关键是当二次函数顶点在x轴下方或当二次函数的顶点在x轴上时分析.

练习册系列答案
相关题目
7. 如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )
如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )
 如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )
如图,在△ABC中,AB=AC,且AE=AD,∠EDC=α,则∠BAD=( )| A. | α | B. | 2α | C. | 3α | D. | 4α |
8.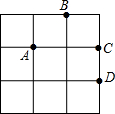 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
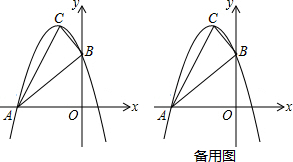
12. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),($\frac{3}{2}$,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①2a+b=0;②b+2c<0;③4a+2b+c<0;④若(0,y1),($\frac{3}{2}$,y2)是抛物线上的两点,那么y1<y2.其中正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
9. 已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为2;
②该函数的一条性质:该函数有最大值.
 已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:| x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
| y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为2;
②该函数的一条性质:该函数有最大值.
7.将抛物线y=(x-3)2-4向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
| A. | y=(x-4)2-6 | B. | y=(x-4)2-2 | C. | y=(x-2)2-2 | D. | y=(x-1)2-3 |
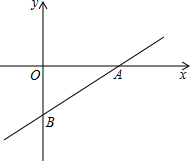 如图,直线y=$\frac{3}{4}$x-3交x轴于点A,交y轴于点B.已知x轴上某一点C到直线y=$\frac{3}{4}$x-3的距离为5,则点C的坐标为($\frac{37}{3}$,0)或(-$\frac{13}{3}$,0).
如图,直线y=$\frac{3}{4}$x-3交x轴于点A,交y轴于点B.已知x轴上某一点C到直线y=$\frac{3}{4}$x-3的距离为5,则点C的坐标为($\frac{37}{3}$,0)或(-$\frac{13}{3}$,0).