题目内容
在菱形ABCD中，对角线AC、BD相交于点O，若AC=6cm，BD=8cm，则菱形ABCD的周长是（ ）
| A、12cm | B、16cm |
| C、20cm | D、40cm |
考点：菱形的性质
专题：
分析：由菱形ABCD中对角线AC、BD相交于点O，若AC=6，BD=8，即可求得OA与OB的长，然后由股定理求得菱形的边长．
解答：
解：∵四边形ABCD是菱形，且AC=6，BD=8，
∴OA=
AB=3，OB=
BD=4，AC⊥BD，
∴AB=
=5．
∴菱形ABCD的周长是20cm，
故选C．
解：∵四边形ABCD是菱形，且AC=6，BD=8，∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
∴菱形ABCD的周长是20cm，
故选C．
点评：本题考查了菱形的性质，解答本题的关键是掌握菱形的对角线互相垂直且平分．
练习册系列答案
应用题作业本系列答案
相关题目
下列四个数中最小的数是（ ）
| A、5 | ||
B、-
| ||
| C、0 | ||
| D、-2 |
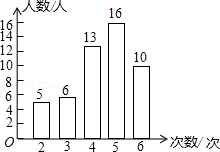（1）某市开展了“寻找雷锋足迹”的活动，某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况，随机调查了七年级50名学生在一个月内做好事的次数，并将所得数据绘制成统计图，请根据图中提供的信息解答下列问题；
下列不等式组中，它的解集在数轴上表示成如图所示，则这个不等式组为（ ）A、
| |||||
B、
| |||||
C、
| |||||
D、
|