题目内容
为了抓住哈尔滨之夏音乐会的商机,某商场决定购进甲、乙两种纪念品,若购进甲种纪念品1件和乙种纪念品2件共需要l70元;若购进甲种纪念品2件和乙种纪念品3件共需要295元.
(1)求购进甲、乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲、乙两种纪念品共l00件,且用于购买这l00件纪念品的资金不超过6670元,则该商场最多能购进甲种纪念品多少件?
(1)求购进甲、乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲、乙两种纪念品共l00件,且用于购买这l00件纪念品的资金不超过6670元,则该商场最多能购进甲种纪念品多少件?
考点:二元一次方程组的应用,一元一次不等式的应用
专题:
分析:(1)设甲种纪念品每件x元,乙种纪念品每件y元,根据购进甲种纪念品1件和乙种纪念品2件共需要l70元,购进甲种纪念品2件和乙种纪念品3件共需要295元,列方程组求解;
(2)设购进甲种纪念品a件,购进乙种纪念品(100-a)件,根据用于购买这l00件纪念品的资金不超过6670元,列不等式求解.
(2)设购进甲种纪念品a件,购进乙种纪念品(100-a)件,根据用于购买这l00件纪念品的资金不超过6670元,列不等式求解.
解答:解:(1)设甲种纪念品每件x元,乙种纪念品每件y元,
由题意得,
,
解得:
,
答:购进甲、乙两种纪念品每件各需要80元、45元.
(2)设购进甲种纪念品a件,购进乙种纪念品(100-a)件,
由题意得,80a+45(200-a)≤6670,
解得:a≤62.
则a最多为62.
答:商场最多购进甲种纪念品62件.
由题意得,
|
解得:
|
答:购进甲、乙两种纪念品每件各需要80元、45元.
(2)设购进甲种纪念品a件,购进乙种纪念品(100-a)件,
由题意得,80a+45(200-a)≤6670,
解得:a≤62.
则a最多为62.
答:商场最多购进甲种纪念品62件.
点评:本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,找出题目所给的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
相关题目
在菱形ABCD中,对角线AC、BD相交于点O,若AC=6cm,BD=8cm,则菱形ABCD的周长是( )
| A、12cm | B、16cm |
| C、20cm | D、40cm |
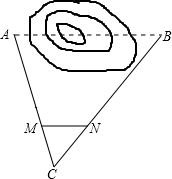 如图,A、B两点被池塘隔开,在AB外任取一点C,连结AC、BC分别取其三等分点M,N(M、N两点均靠近点C).量得MN=27m,则AB的长是( )
如图,A、B两点被池塘隔开,在AB外任取一点C,连结AC、BC分别取其三等分点M,N(M、N两点均靠近点C).量得MN=27m,则AB的长是( )| A、54m | B、81m |
| C、108m | D、135m |
把下列各数填在相应的大括号内:
-5,|-
|,-12,0,-3.14,+1.99,-(-6),
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
-5,|-
| 3 |
| 4 |
| 22 |
| 7 |
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
 如图,该图形的面积是( )
如图,该图形的面积是( )A、
| ||
B、
| ||
| C、6xy | ||
| D、3xy |