题目内容

5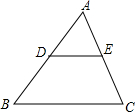．如图，点D、E分别为△ABC的边AB、AC上的中点，则△ADE的面积与四边形BCED的面积的比为（　　）
A．1：2B．1：3C．1：4D．1：1

分析 证明DE是△ABC的中位线，由三角形中位线定理得出DE∥BC，DE=$\frac{1}{2}$BC，证出△ADE∽△ABC，由相似三角形的性质得出△ADE的面积：△ABC的面积=1：4，即可得出结果．

解答 解：∵D、E分别为△ABC的边AB、AC上的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∴△ADE∽△ABC，
∴△ADE的面积：△ABC的面积=（$\frac{1}{2}$）2=1：4，
∴△ADE的面积：四边形BCED的面积=1：3；
故选：B．

点评 本题考查了相似三角形的判定与性质、三角形中位线定理；熟记三角形中位线定理，证明三角形相似是解决问题的关键．

练习册系列答案
相关题目
15．已知a2-2a-2=0，求代数式$\frac{2}{{{a^2}-1}}÷\frac{a-1}{a+1}$的值．
16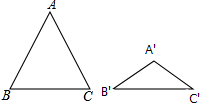．如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为（　　）
A．25：9B．5：3C．$\sqrt{5}$：$\sqrt{3}$D．5$\sqrt{5}$：3$\sqrt{3}$
13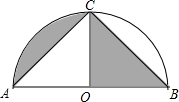．如图，以AB为直径，点O为圆心的半圆经过点C，若AC=BC=$\sqrt{2}$，则图中阴影部分的面积是（　　）
A．$\frac{π}{4}$B．$\frac{1}{2}$$+\frac{π}{4}$C．$\frac{π}{2}$D．$\frac{1}{2}$+$\frac{π}{2}$
20．如图，在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C，灯塔C距码头的东端N有20km．一轮船以36km/h的速度航行，上午10：00在A处测得灯塔C位于轮船的北偏西30°方向，上午10：40在B处测得灯塔C位于轮船的北偏东60°方向，且与灯塔C相距12km．
（1）若轮船照此速度与航向航行，何时到达海岸线？
（2）若轮船不改变航向，该轮船能否停靠在码头？请说明理由．（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）
10．先化简：$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$÷（$\frac{2}{x-1}$-$\frac{1}{x}$），然后再从-2＜x≤2的范围内选取一个合适的x的整数值代入求值．
17．如图所示几何体的俯视图是（　　）
A．B．C．D．
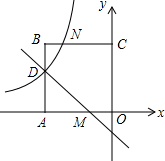14．如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的图象过点D和M，反比例函数y=$\frac{m}{x}$的图象经过点D，与BC的交点为N．
（1）求反比例函数和一次函数的表达式；
（2）若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．
15．半径为6，圆心角为120°的扇形的面积是（　　）
A．3πB．6πC．9πD．12π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网