题目内容
19．已知△ABC的三边长a、b、c满足$\sqrt{a-1}$+|b-$\sqrt{3}$|+（c-2）2=0，则△ABC一定是直角三角形．分析 先根据非负数的性质求出a、b、c的值，再根据勾股定理的逆定理进行解答即可．
解答 解：∵△ABC的三边长a、b、c满足$\sqrt{a-1}$+|b-$\sqrt{3}$|+（c-2）2=0，
∴a=1，b=$\sqrt{3}$，c=2，
∵12+（$\sqrt{3}$）2=22，
∴△ABC是直角三角形，
故答案为直角．
点评 本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
练习册系列答案
相关题目
9．下列说法正确的是（ ）
①最大的负整数是-1；
②数轴上表示数4和-4的点到原点的距离相等；
③当a≤0时，|a|=-a成立；
④a的倒数是$\frac{1}{a}$；
⑤（-2）3和-23相等．
①最大的负整数是-1；
②数轴上表示数4和-4的点到原点的距离相等；
③当a≤0时，|a|=-a成立；
④a的倒数是$\frac{1}{a}$；
⑤（-2）3和-23相等．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
10．
如图，四边形ABCD的四个顶点都在圆上，若∠A=100°，则∠C的度数是（ ）
如图，四边形ABCD的四个顶点都在圆上，若∠A=100°，则∠C的度数是（ ）| A． | 60° | B． | 80° | C． | 90° | D． | 100° |
7．一只蚂蚁从数轴表示数-2的点A出发，向右直爬5个单位到达点B，则点B所表示的数为（ ）
| A． | 5 | B． | 3 | C． | -3 | D． | -1 |
4．一元二次方程2x2+x-3=0的根的情况是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 没有实数根 | D． | 无法确定 |
8．
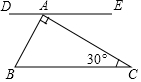如图，一块含30°角的直角三角板ABC的直角顶点A在直线DE上，且BC∥DE，则∠DAB等于（ ）
如图，一块含30°角的直角三角板ABC的直角顶点A在直线DE上，且BC∥DE，则∠DAB等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |