题目内容
8．
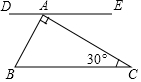如图，一块含30°角的直角三角板ABC的直角顶点A在直线DE上，且BC∥DE，则∠DAB等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 根据三角形内角和定理求出∠B，根据平行线的性质得出∠DAB=∠B，即可得出选项．
解答 解：∠BAC=90°，∠C=30°，
∴∠B=180°-∠BAC-∠C=60°，
∵BC∥DE，
∴∠DAB=∠B=60°，
故选C．
点评 本题考查了平行线的性质和三角形内角和定理的应用，能灵活运用定理进行推理和计算是解此题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
3．
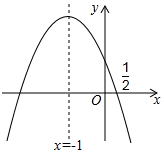如图，抛物线y=ax2+bx+c的对称轴是x=-1．且过点（$\frac{1}{2}$，0），有下列结论：①abc＞0；
②a-2b+4c=0； ③25a-10b+4c=0； ④3b+2c＞0； ⑤a-b≥m（am-b）；
其中所有正确的结论是（ ）
如图，抛物线y=ax2+bx+c的对称轴是x=-1．且过点（$\frac{1}{2}$，0），有下列结论：①abc＞0； ②a-2b+4c=0； ③25a-10b+4c=0； ④3b+2c＞0； ⑤a-b≥m（am-b）；
其中所有正确的结论是（ ）
| A． | ①②③ | B． | ①③④ | C． | ①②③⑤ | D． | ①③⑤ |
13．计算：（-3）+5的结果是（ ）
| A． | -2 | B． | 2 | C． | 8 | D． | -8 |
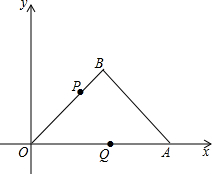如图，∠OAB=45°，点A的坐标是（4，0），AB=$2\sqrt{2}$，连结OB．