题目内容
17.如果x=y,a为有理数,那么下列等式不一定成立的是( )| A. | 4-y=4-x | B. | x2=y2 | C. | $\frac{x}{a}=\frac{y}{a}$ | D. | -2ax=-2ay |
分析 A、等式两边先同时乘-1,然后再同时加4即可;
B、根据乘方的定义可判断;
C、根据等式的性质2判断即可;
D、根据等式的性质2判断即可.
解答 解:A、∵x=y,
∴-x=-y.
∴-x+4=-y+4,即4-y=4-x,故A一定成立,与要求不符;
B、如果x=y,则x2=y2,故B一定成立,与要求不符;
C、当a=0时,$\frac{x}{a}=\frac{y}{a}$无意义,故C不一定成立,与要求相符;
D、由等式的性质可知:-2ax=-2ay,故D一定成立,与要求不符.
故选:C.
点评 本题主要考查的是等式的性质,掌握等式的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
2.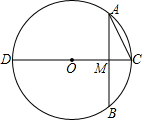 如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
 如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )
如图,已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长度为( )| A. | 4$\sqrt{5}$cm | B. | 3$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm | D. | $\sqrt{5}$cm |
 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF.
如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF. 如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于100°.
如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠AOB等于100°. 如图,将△ABC纸片折叠,使点A落在边BC上,记落点为点D,且折痕EF∥BC,若EF=3,则BC的长度为6.
如图,将△ABC纸片折叠,使点A落在边BC上,记落点为点D,且折痕EF∥BC,若EF=3,则BC的长度为6.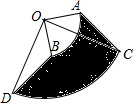 如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.