题目内容
6.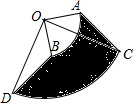 如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若$\widehat{AB}$的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
分析 (1)根据旋转的定义求解;
(2)先利用弧长公式计算出OA=2,再根据旋转的性质得到△AOC≌△BOD,则S△AOC=S△BOD,接着根据S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分得到S阴影部分=S扇形COD-S扇形AOB,然后利用扇形的面积公式计算即可.
解答 解:(1)∵扇形OAB和扇形OCD的圆心角都是90°,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴将△AOC绕点O顺时针旋转90°可以得到△BOD;
(2)∵$\frac{90•π•OA}{180}$=π,
∴OA=2,
∵△AOC绕点O顺时针旋转90°可以得到△BOD,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∵S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,
∴S阴影部分=S扇形COD-S扇形AOB=$\frac{90•π•{3}^{2}}{360}$-$\frac{90•π•{2}^{2}}{360}$=$\frac{5}{4}$π(cm2).
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了扇形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列各式从左到右的变形,属于因式分解的是( )
| A. | a2-b2=(a-b)(a+b) | B. | mx+my+nx+ny=m(x+y)+n(x+y) | ||
| C. | (x+1)(x-1)=x2-1 | D. | x2-2x+1=x(x-2)+1 |
17.如果x=y,a为有理数,那么下列等式不一定成立的是( )
| A. | 4-y=4-x | B. | x2=y2 | C. | $\frac{x}{a}=\frac{y}{a}$ | D. | -2ax=-2ay |
14. 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=82°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=82°,则∠4等于( )
 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=82°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=82°,则∠4等于( )| A. | 41° | B. | 51° | C. | 60° | D. | 81° |
16.在半径为5cm的⊙O中,点P是⊙O内一点,且OP=3cm,则过点P的最短弦长是( )
| A. | 4cm | B. | 3cm | C. | 6cm | D. | 8cm |
 已知,线段AB=12,点O是AB的中点,C是线段AO上一点,且OC:OB=1:3,求线段AC的长.
已知,线段AB=12,点O是AB的中点,C是线段AO上一点,且OC:OB=1:3,求线段AC的长. 如图,用总长度为12米的不锈钢材料设计成如图所示的外观为矩形的框架,所有横档和竖档分别与AD、AB平行,则矩形框架ABCD的最大面积为4m2.
如图,用总长度为12米的不锈钢材料设计成如图所示的外观为矩形的框架,所有横档和竖档分别与AD、AB平行,则矩形框架ABCD的最大面积为4m2.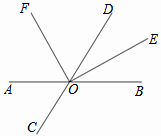 如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF是∠AOD的平分线.