题目内容
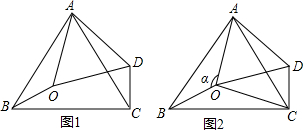
9．
如图，将△ABC纸片折叠，使点A落在边BC上，记落点为点D，且折痕EF∥BC，若EF=3，则BC的长度为6．
分析 连接AD交EF于点G，由轴对称的性质可知，EF垂直平分AD，得出EF为△ABC的中位线，得出答案即可．
解答 解：如图，
连接AD交EF于点G，由轴对称的性质可得
EF垂直平分AD，且G为AD中点，
∵EF∥BC，
∴E、F分别为AB、AC的中点，
∴BC=2EF=2×3=6．
故答案为：6．
点评 此题考查了折叠的性质与三角形的中位线的性质定理，证明EF是△ABC的中位线是关键．
练习册系列答案
相关题目
19．
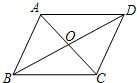如图，四边形ABCD的对角线AC，BD交于O点，且AB$\stackrel{∥}{=}$CD，那么图中的全等三角形有（ ）
如图，四边形ABCD的对角线AC，BD交于O点，且AB$\stackrel{∥}{=}$CD，那么图中的全等三角形有（ ）| A． | 2对 | B． | 3对 | C． | 4对 | D． | 5对 |
17．如果x=y，a为有理数，那么下列等式不一定成立的是（ ）
| A． | 4-y=4-x | B． | x2=y2 | C． | $\frac{x}{a}=\frac{y}{a}$ | D． | -2ax=-2ay |
14．
如图，直线a，b被直线c所截，a∥b，∠2=∠3，若∠1=82°，则∠4等于（ ）
如图，直线a，b被直线c所截，a∥b，∠2=∠3，若∠1=82°，则∠4等于（ ）| A． | 41° | B． | 51° | C． | 60° | D． | 81° |
已知，线段AB=12，点O是AB的中点，C是线段AO上一点，且OC：OB=1：3，求线段AC的长．