题目内容
17.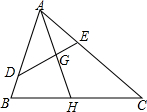 如图,D是△ABC的边AB上一点,∠ADE=∠C,DE交AC于点E,AH为△ABC的角平分线,AH交DE于点G,已知AE=2,AB=4,求$\frac{AG}{AH}$的值.
如图,D是△ABC的边AB上一点,∠ADE=∠C,DE交AC于点E,AH为△ABC的角平分线,AH交DE于点G,已知AE=2,AB=4,求$\frac{AG}{AH}$的值.
分析 利用AH为△ABC的角平分线,得出∠BAH=∠HAC,证得△ABH∽△AEG,得出$\frac{AE}{AB}$=$\frac{AG}{AH}$求得答案.
解答 解:∵AH为△ABC的角平分线,
∴∠BAH=∠HAC,
又∵∠ADE=∠C,
∴∠B=∠AED,
∴△AEG∽△ABH,
∴$\frac{AG}{AH}$=$\frac{AE}{AB}$=$\frac{1}{2}$.
点评 此题考查相似三角形的判定与性质,掌握相似三角形的判定方法是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
8.在二次函数y=x2+bx+c中,函数值y与自变量x的部分对应值如表,则该抛物线的顶点坐标为(1,-2),m=-1.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 7 | 2 | -1 | -2 | m | 2 | 7 |
12.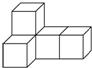 如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )
如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )
 如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )
如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )| A. | 从正面看所得到的形状图的面积最小 | |
| B. | 从左面看所得到的形状图的面积最小 | |
| C. | 从上面看所得到的形状图的面积最小 | |
| D. | 从三个方向看所得到的形状图的面积一样大 |
2.已知正比例函数y=kx的图象经过(1,-2)点,则k=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
9.九年级某班5名女同学的体重(单位:kg)分别为35,40,37,42,42,则这组数据的中位数是( )
| A. | 35 | B. | 37 | C. | 40 | D. | 42 |
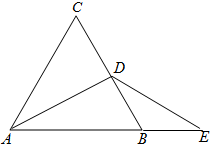 如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD.
如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD. 已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小?
已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小?