题目内容
7. 已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小?
已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小?
分析 延长BD交x轴于E,根据已知条件得到AB=AE,由等腰三角形的性质得到BD=DE,求出∠ABO=∠BAO=45°,得到∠AED=67.5°,根据直角三角形的性质得到DE=DO,于是求得∠DEO=∠DOE=67.5°,即可得到结论.
解答  解:延长BD交x轴于E,
解:延长BD交x轴于E,
∵AD平分∠BAO,BD⊥AD于D,
∴AB=AE,
∴BD=DE,
∵A(3,0),B(0,3),
∴OA=OB=3,
∴∠ABO=∠BAO=45°,
∴$∠DAE=\frac{1}{2}∠OAB$=22.5°,
∴∠AED=67.5°,
∵∠BOE=90°,
∴DE=DO,
∴∠DEO=∠DOE=67.5°,
∴∠ADO=67.5°-22.5°=45°.
点评 本题考查了等腰三角形的判定和性质,等腰直角三角形的性质,直角三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
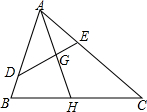 如图,D是△ABC的边AB上一点,∠ADE=∠C,DE交AC于点E,AH为△ABC的角平分线,AH交DE于点G,已知AE=2,AB=4,求$\frac{AG}{AH}$的值.
如图,D是△ABC的边AB上一点,∠ADE=∠C,DE交AC于点E,AH为△ABC的角平分线,AH交DE于点G,已知AE=2,AB=4,求$\frac{AG}{AH}$的值.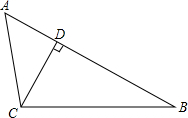 如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证:
如图所示,在△ABC中,CD是AB边上的高,且AC•BD=BC•CD.求证: 已知,如图,点E是平行四边形ABCD的边CD上一点,直线BF交AD的延长线于点E,求证:BF:BE=BC:AE.
已知,如图,点E是平行四边形ABCD的边CD上一点,直线BF交AD的延长线于点E,求证:BF:BE=BC:AE. 如图.点D、E分别是等边△ABC边AB、BC上的点(D、E不与△ABC顶点重合).且∠DEF=60°,求证:△DBE∽△ECF.
如图.点D、E分别是等边△ABC边AB、BC上的点(D、E不与△ABC顶点重合).且∠DEF=60°,求证:△DBE∽△ECF.