题目内容
11.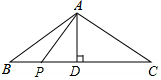 如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).
如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).(1)求AD的长;
(2)当t=12s时,PC=AC;
(3)当△PAC是直角三角形时,求t的值.
分析 (1)根据等腰三角形三线合一性质可得到BD的长,由勾股定理可求得AD的长;
(2)先求出P点移动的路程BP,再除以速度即可;
(3)分两种情况进行分析:①PA⊥AC②PA⊥BC,从而可得到运动的时间.
解答  解:(1)∵等腰△ABC的底边BC=8cm,AD是底边BC上的高,
解:(1)∵等腰△ABC的底边BC=8cm,AD是底边BC上的高,
∴BD=CD=$\frac{1}{2}$BC=4cm,
∵腰AC=5cm,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3cm;
(2)∵PC=AC=5cm,
∴BP=BC-PC=3cm,
∵动点P在底边上从点B开始向点C以0.25cm/s的速度移动,
∴t=3÷0.25=12s.
故答案为12;
(3)分两种情况:
①当点P运动t秒后有PA⊥AC时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,
∴PD=2.25,
∴BP=4-2.25=1.75=0.25t,
∴t=7秒;
当点P运动t秒后有PA⊥BC时,即P与D重合,
∵BP=BD=4=0.25t,
∴t=16秒,
∴点P运动的时间为7秒或16秒.
点评 本题考查了等腰三角形的性质,勾股定理,利用数形结合以及分类讨论是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.平面直角坐标系中,与点(-5,8)关于y轴对称的点的坐标是( )
| A. | (5,-8) | B. | (-5,-8) | C. | (5,8) | D. | (8,-5) |
2.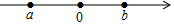 实数a,b,在数轴上大致位置如图,则a,b,的大小关系是( )
实数a,b,在数轴上大致位置如图,则a,b,的大小关系是( )
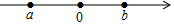 实数a,b,在数轴上大致位置如图,则a,b,的大小关系是( )
实数a,b,在数轴上大致位置如图,则a,b,的大小关系是( )| A. | a<0<b | B. | b<a<0 | C. | 0<b<a | D. | a>0>b |
1.对于非零向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$下列条件中,不能判定$\overrightarrow{a}$与$\overrightarrow{b}$是平行向量的是( )
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{c}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+3$\overrightarrow{c}$=$\overrightarrow{0}$,$\overrightarrow{b}$=3$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-3$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=3|$\overrightarrow{b}$| |
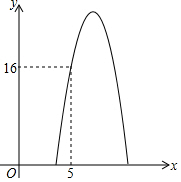 某商品的进价为每个3元,已知该商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=ax2+16x+c,其图象如图所示.
某商品的进价为每个3元,已知该商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=ax2+16x+c,其图象如图所示.