题目内容
16.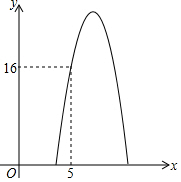 某商品的进价为每个3元,已知该商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=ax2+16x+c,其图象如图所示.
某商品的进价为每个3元,已知该商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=ax2+16x+c,其图象如图所示.(1)求a、c的值;
(2)销售单价为多少元时,该商品每天的销售利润最大?最大利润为多少元?
(3)销售单价在什么范围时,该商品每天的销售利润不低于16元?
分析 (1)利用待定系数法求二次函数解析式得出即可;
(2)利用配方法求出二次函数最值即可;
(3)根据题意令y=16,解方程可得x的值,结合图象可知x的范围.
解答 解:(1)y=ax2+16x+c图象过点(3,0)、(5,16),
∴$\left\{\begin{array}{l}{9a+48+c=0}\\{25a+80+c=16}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{c=-39}\end{array}\right.$.
(2)∵y=-x2+16x-39=-(x-8)2+25,
∴当x=8时,y最大=25.
答:销售单价为8元时,该种商品每天的销售利润最大,最大利润为25元;
(3)根据题意,当y=16时,得:-x2+16x-39=16,
解得:x1=5,x2=11,
即销售单价5≤x≤11时,该种商品每天的销售利润不低于16元.
点评 本题考查了二次函数的应用以及待定系数法求二次函数解析式等知识,正确利用二次函数图象是解题关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.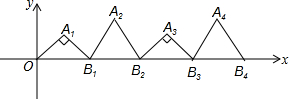 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )| A. | (4029,1) | B. | (2015,$\sqrt{3}$) | C. | (4030,1) | D. | (4029,$\sqrt{3}$) |
5.将235000000用科学记数法表示为( )
| A. | 235×106 | B. | 2.35×107 | C. | 2.35×108 | D. | 0.235×109 |
 如图,已知点B,C,F,E在同一直线上,AB=DE,BC=EF,AB∥DE.求证:AC∥DF.
如图,已知点B,C,F,E在同一直线上,AB=DE,BC=EF,AB∥DE.求证:AC∥DF. 如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.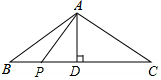 如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).
如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).