题目内容
3.若x=-2是方程3x-k=k(x-2)的根,(a-3)2+|b+3|=0,且代数式$\frac{ka-b+n}{2}$的值比代数式$\frac{2}{27}$ab2+$\frac{1}{6}$n的值大1,试求n的值.分析 根据非负数的性质求得a=3,b=-3,把x=-2代入方程3x-k=k(x-2)的根,求的k的值,然后根据$\frac{ka-b+n}{2}$的值比代数式$\frac{2}{27}$ab2+$\frac{1}{6}$n的值大1即可列方程求得n的值.
解答 解:∵(a-3)2+|b+3|=0,
∴a=3,b=-3,
把x=-2代入3x-k=k(x-2)得:-4k=-6-k,
解得:k=2.
则$\frac{6+3+n}{2}$-1=$\frac{2}{27}$×3×9+$\frac{1}{6}$n,
解得n=-4.5.
点评 本题考查了非负数的性质以及方程的解的定义,方程的解就是能使方程左右两边相等的未知数的值,求得a、b、k的值是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
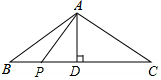 如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s).
如图,等腰△ABC的底边BC=8cm,腰AC=5cm,AD是底边BC上的高,一动点P在底边上从点B开始向点C以0.25cm/s的速度移动,设运动时间为t(s). 如图,在平面直角坐标系中xOy中,抛物线y=-x2+bx+c与x轴相交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D,联结AC、BC、DB、DC.
如图,在平面直角坐标系中xOy中,抛物线y=-x2+bx+c与x轴相交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D,联结AC、BC、DB、DC.