题目内容
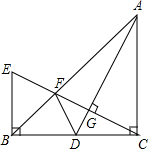 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作B C的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②AB=CE;③∠ADC=∠BDF;④F为EG中点.其中结论正确的个数为( )
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作B C的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②AB=CE;③∠ADC=∠BDF;④F为EG中点.其中结论正确的个数为( )| A、1 | B、2 | C、3 | D、4 |
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:①由条件可知∠ECD+∠ADC=∠E+∠ECD=90°,可得到∠E=∠ADC,再结合条件可证明△ADC≌△CEB;②由①可知CE=AD,显然AB>AD,故AB≠CE;③BE=CD=BD,结合条件可证明△BEF≌△BDF,则有∠E=∠BDF=∠ADC,可得结论;④由③可得EF=DF,而DF>FG,故F不可能为EG中点.
解答:解:
∵∠BCA=90°,CG⊥AD,
∴∠ECD+∠ADC=∠E+∠ECD=90°,
∴∠E=∠ADC,
∵BE⊥BC,
∴∠EBC=∠ACD,
在△ADC和△CEB中
∴△ADC≌△CEB(AAS),
∴①正确;
∵△ADC≌△CEB,
∴CE=AD,
在△ABD中,AB>AD,
∴AB≠CE,
∴②不正确;
∵△ADC≌△CEB,且D为BC中点,
∴BE=CD=BD,
∵AC=BC,∠ACB=90°,
∴∠DBF=∠EBF=45°,
在△BEF和△BDF中
∴△BEF≌△BDF(SAS),
∴∠E=∠BDF,又∠E=∠ADC,
∴∠ADC=∠BDF,
∴③正确;
∵△BEF≌△BDF,
∴EF=DF,
在R△DFG中,DF>FG,
∴EF>FG,
∴F不是EG的中点,
∴④不正确;
综上可知正确的有①③共两个,
故选B.
∵∠BCA=90°,CG⊥AD,
∴∠ECD+∠ADC=∠E+∠ECD=90°,
∴∠E=∠ADC,
∵BE⊥BC,
∴∠EBC=∠ACD,
在△ADC和△CEB中
|
∴△ADC≌△CEB(AAS),
∴①正确;
∵△ADC≌△CEB,
∴CE=AD,
在△ABD中,AB>AD,
∴AB≠CE,
∴②不正确;
∵△ADC≌△CEB,且D为BC中点,
∴BE=CD=BD,
∵AC=BC,∠ACB=90°,
∴∠DBF=∠EBF=45°,
在△BEF和△BDF中
|
∴△BEF≌△BDF(SAS),
∴∠E=∠BDF,又∠E=∠ADC,
∴∠ADC=∠BDF,
∴③正确;
∵△BEF≌△BDF,
∴EF=DF,
在R△DFG中,DF>FG,
∴EF>FG,
∴F不是EG的中点,
∴④不正确;
综上可知正确的有①③共两个,
故选B.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法SSS、SAS、ASA、AAS和HL是解题的关键.

练习册系列答案
相关题目
 如图,AB,CD是⊙O的弦,连接AC,AC与BD相交于点E,证明:△ABE∽△DCE.
如图,AB,CD是⊙O的弦,连接AC,AC与BD相交于点E,证明:△ABE∽△DCE. 如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.
如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线. 已知:如图,AB=AD,∠B=∠D,∠1=∠2=60°,求证:AE=EC.
已知:如图,AB=AD,∠B=∠D,∠1=∠2=60°,求证:AE=EC.