题目内容
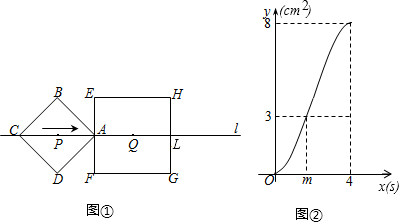
3.如图①正方形ABCD,EFGH的中心P、Q都在直线l上,EF⊥l,AC∥EH,正方形ABCD以1cm/s的速度沿直线l向正方形EFGH移动,当点A与HG的中点L重合时停止移动,设移动时间为xs时,这两个正方形重叠部分面积为ycm2,y与x的函数图象如图②,则下列结论:①AC=4cm;②当x=3t时重叠部分的面积为7cm2;③m=$\sqrt{3}$s;④当P、Q重合时,重叠部分的面积为8cm2;⑤当2<x≤4时,y与x的函数关系式是y=-(x-4)2+8;
其中正确的结论的序号是①②③④⑤(把所有正确结论的序号都填在横线上)
分析 ①由这两个正方形的重叠部分面积为8时,也就是小正方形的面积为8,求出边长即可得出AC的长;
②当2≤x≤6时,得到y与x的函数关系式,当y=7时,解方程可作判断;
③当6≤x≤8时,y与x的函数关系式为y=(8-x)2,此时函数y的取值范围是0≤y≤4.当y=3时,解方程即可求出m;
④由图象可得结论;
⑤当2≤x≤6时,y与x的函数关系式为y=-(x-4)2+8.
解答 解:(1)当这两个正方形的重叠部分面积为8时,也就是小正方形的面积为8,得出小正方形的边长为2$\sqrt{2}$cm,所以AC=$\sqrt{2}$×2$\sqrt{2}$=4cm,故①正确.
(2)当2≤x≤6时,y与x的函数关系式为y=-(x-4)2+8,此时函数y的取值范围是4≤y≤8,当y=7时,得-(x-4)2+8=7,解得x=3或x=5.所以正方形ABCD出发3秒或5秒时,重叠部分面积为7cm2,故②正确;
(3)当0≤x≤2时,y与x的函数关系式为y=x2,此时函数y的取值范围是0≤y≤4,当y=3时,得x2=3或(8-x)2=3,解得x=±$\sqrt{3}$(负号舍去)或x=±$\sqrt{3}$+8(正号舍去),即m=$\sqrt{3}$,故③正确;
(4)由图象可以看出两个正方形的最大重叠部分面积为8,此时P、Q重合,故④正确;
(5)当2≤x≤6时,y与x的函数关系式为y=-(x-4)2+8,故⑤正确;
故答案为:①②③④⑤.
点评 本题主要考查了动点问题的函数图象,解题的关键是通过图形获取信息,要理清图象的含义即会识图.

练习册系列答案
相关题目
12.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2有增根,则m的值是( )
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
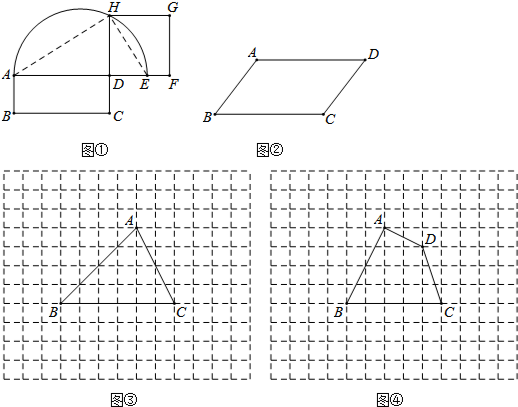
14.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为( )
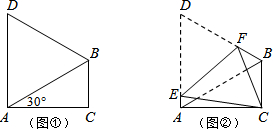

| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
18.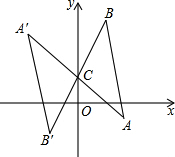 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
 如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )| A. | (-a,-b) | B. | (-a,-b+2) | C. | (-a,-b+1) | D. | (-a,-b-1) |
12.如图1所示,?ABCD中,动点P从点B出发,沿BC,CD运动至点D停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的图象如图2所示,则?ABCD的面积是( )
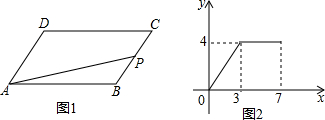

| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
13.某公司招聘人才,对应聘者分别进行阅读能力,思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
| 项目 人员 | 阅读 | 思维 | 表达 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
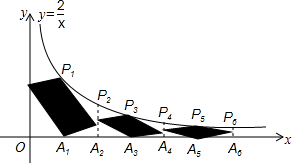 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上有点P1,P2,P3,…,它们的横坐标依次为1,2,3,…,分别过这些点作x轴的垂线,垂足依次为A1,A2,A3,…,分别以P1A1,P3A3,P5A5…为对角线作平行四边形,另两顶点分别落在P2n-2A2n-2与P2nA2n上(n=1,2,3,…,P0A0为y轴),所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,记P1=$\frac{1}{{S}_{1}}$,P2=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$,P3=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$,…,则P2=2;Pn-Pn-1=$\frac{2n-1}{2}$.