题目内容
8.不等式组$\left\{\begin{array}{l}{2x+4>0}\\{\frac{x+2}{3}≥x}\end{array}\right.$的整数解有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式2x+4>0,得:x>-2,
解不等式$\frac{x+2}{3}$≥x,得:x≤1,
则不等式组的解集为-2<x≤1,
∴不等式组的整数解有-1、0、1这3个,
故选:C.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
3.若代数式$\frac{2}{x-3}$在实数范围内有意义,则x的取值范围是( )
| A. | x<3 | B. | x>3 | C. | x≠3 | D. | x≠-3 |
13.下列运算正确的是( )
| A. | 2a2-4a2=-2 | B. | (-b3)2=-b6 | C. | (xy)2÷(-xy)=-xy | D. | (m-n)2=m2-n2 |
20.将抛物线y=2x2-2向左平移1个单位,再向上平移3个单位就得到抛物线( )
| A. | y=2(x+1)2-5 | B. | y=2(x-1)2+1 | C. | y=2(x+1)2+1 | D. | y=2(x-1)2-5 |
17.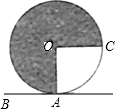 如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )
如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )
 如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )
如图,⊙O的半径是1,AB是⊙O的切线,A是切点,若半径OC∥AB,则阴影部分的面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
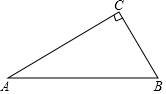 如图,△ABC中,∠C=90°,∠A=30°
如图,△ABC中,∠C=90°,∠A=30°