题目内容
15.已知y=(m+2)x|m+3|+n-2.(1)当m,n为何值时,y是x的正比例函数?
(2)当m,n为何值时,y是x的一次函数?
分析 (1)根据正比例函数的定义得到:|m+3|=1且m+2≠0,n-2=0,由此求得m、n的值;
(2)根据一次函数的定义得到:|m+3|=1且m+2≠0,n-2≠0,由此求得m、n的值.
解答 解:(1)依题意得:|m+3|=1且m+2≠0,n-2=0,
解得m=-4,n=2;
(2)依题意得:|m+3|=1且m+2≠0,n-2≠0,
解得m=-4,n≠2.
点评 本题考查了正比例函数的定义,一次函数的定义,熟记函数的一般形式即可解答,属于基础题.

练习册系列答案
相关题目
14.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
这15名员工每人所创年利润的众数、中位数分别是( )
| 部门 | 人数 | 每人所创年利润(单位:万元) |
| A | 1 | 10 |
| B | 3 | 8 |
| C | 7 | 5 |
| D | 4 | 3 |
| A. | 10,5 | B. | 7,8 | C. | 5,6.5 | D. | 5,5 |
5.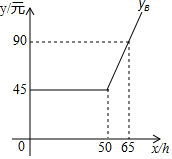 某网站策划了A、B两种上网的月收费方式:
某网站策划了A、B两种上网的月收费方式:
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)
(1)m=45;n=50p=0.05.
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
 某网站策划了A、B两种上网的月收费方式:
某网站策划了A、B两种上网的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | m | n | P |
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)
(1)m=45;n=50p=0.05.
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
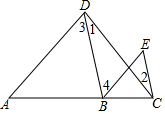 已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE. 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.