题目内容
4. 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.(1)求证:AG与⊙O相切;
(2)若AC=5,AB=12,BE=$\frac{13}{3}$,求线段OE的长.
分析 (1)根据EF⊥BC,得∠BFE=90°,由对顶角相等和等边对等角可得:∠BAO+∠GAE=90°,OA⊥AG,即AG与⊙O相切;
(2)证明△BEF∽△BCA,列比例式得:$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{EF}{CA}$,可求得EF和BF的长,利用勾股定理求OE的长.
解答 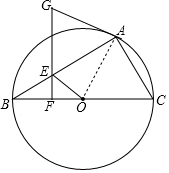 证明:(1)如图,连接OA,
证明:(1)如图,连接OA,
∵OA=OB,GA=GE,
∴∠ABO=∠BAO,∠GEA=∠GAE,
∵EF⊥BC,
∴∠BFE=90°,
∴∠ABO+∠BEF=90°.
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF,
∴∠BAO+∠GAE=90°,
∴OA⊥AG,
即AG与⊙O相切;
(2)解:∵BC为直径,
∴∠BAC=90°,
∵AC=5,AB=12,
∴BC=13,
∵∠EBF=∠CBA,∠BFE=∠BAC,
∴△BEF∽△BCA,
∴$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{EF}{CA}$,
∴$\frac{BF}{12}=\frac{\frac{13}{3}}{13}=\frac{EF}{5}$,
∴EF=$\frac{5}{3}$,BF=4,
∴OF=OB-BF=$\frac{13}{2}$-4=$\frac{5}{2}$,
∴OE=$\sqrt{E{F}^{2}+O{F}^{2}}$=$\frac{5}{6}\sqrt{13}$.
点评 本题考查了切线的判定、三角形相似的性质和判定、勾股定理,熟练掌握切线的判定是关键,证明切线的常见的辅助线作法有:①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;②有切线时,常常“遇到切点连圆心得半径”.

练习册系列答案
相关题目
13.小洪根据演讲比赛中九位评委所给的分数制作了如表:
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是中位数.
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
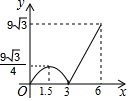
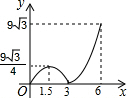
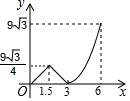
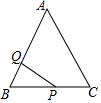 如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )
如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )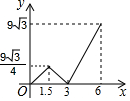

 一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的坐标为(2,1).
一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的坐标为(2,1).