题目内容
9.如图,在平面直角坐标系中A($\sqrt{3}$,0),B(0,1),点P为△OAB内任一点,连PO、PA、PB,将△ABP绕着点A顺时针旋转60°得到△AB′P′,连PP′.(1)求点B′的坐标;
(2)当△OPA与△APB满足什么条件时,PO+PA+PB的值最小,并求出此最小值;
(3)试直接写出(2)中的点P坐标.
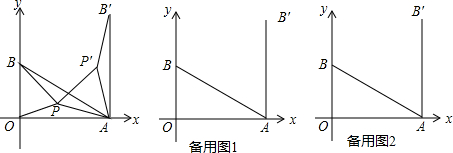
分析 (1)根据点A、B的坐标求得AB的长,再根据旋转角度为60°,求得点B′的坐标;
(2)根据两点之间线段最短,求得PO+PA+PB的最小值;
(3)先将(2)中的△OPB绕着点O逆时针旋转60°,求得点B″的坐标,再根据点P为OB′与AB″的交点,联立方程组求得交点P的坐标即可.
解答 解:(1)∵A($\sqrt{3}$,0),B(0,1)
∴AB=2,∠BAO=30°
∵将△ABP绕着点A顺时针旋转60°得到△AB′P′
∴AB′=2,∠B′AO=90°
∴B′($\sqrt{3}$,2)
(2)由旋转可得,△APP′是等边三角形
∴PP′=PA
又∵P′B′=PB
∴PO+PA+PB=PO+PP′+P′B′
∴如图,当O、P、P′、B′四点共线时,PO+PA+PB的值最小
∴当∠OPA=∠APB=∠AP′B′=120°时,PO+PA+PB的值最小
此时,PO+PA+PB=OB′=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$
(3)如图,将(2)中的△OPB绕着点O逆时针旋转60°得到△OB″P″,则∠BOB″=60°,OB″=OB=1
∴点B的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)
由(2)可知A、P、P″、B″四点共线
∴点P为OB′与AB″的交点
根据A、B″两点的坐标可得直线AB″的解析式为y=-$\frac{\sqrt{3}}{9}$x+$\frac{1}{3}$
根据B′的坐标可得直线OB′的解析式为y=$\frac{2\sqrt{3}}{3}$x
联立方程组,解得P($\frac{\sqrt{3}}{7}$,$\frac{2}{7}$)
点评 本题主要考查了几何变换中的旋转变换,解题的关键是掌握旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角.在求最小值时,往往需要考虑两点之间线段最短或者垂线段最短等基本结论,在求两直线交点坐标时,需要联立方程组进行求解.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | 无实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 根的情况不确定 |
 如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.
如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.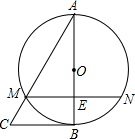 如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=$\sqrt{3}$,则弧BN的长为$\frac{2\sqrt{3}}{9}$π.
如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=$\sqrt{3}$,则弧BN的长为$\frac{2\sqrt{3}}{9}$π.