题目内容
4.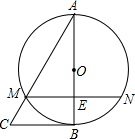 如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=$\sqrt{3}$,则弧BN的长为$\frac{2\sqrt{3}}{9}$π.
如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=$\sqrt{3}$,则弧BN的长为$\frac{2\sqrt{3}}{9}$π.
分析 先根据勾股定理判断出△AME的形状,再由垂径定理得出$\widehat{BN}$=$\widehat{BM}$,由锐角三角函数的定义求出∠A的度数,故可得出∠MOB的度数,求出OM的长,再根据弧长公式即可得出结论.
解答 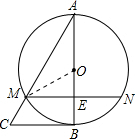 解:∵△AME中,ME=1,AM=2,AE=$\sqrt{3}$,
解:∵△AME中,ME=1,AM=2,AE=$\sqrt{3}$,
∴AE2+ME2=AM2,
∴△AME是直角三角形,即AE⊥MN,
∵sinA=$\frac{ME}{AM}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠MOB=60°,
∴$\frac{ME}{OM}$=sin∠MOB,即$\frac{1}{OM}$=$\frac{\sqrt{3}}{2}$,
解得OM=$\frac{2\sqrt{3}}{3}$,
∵AE⊥MN,
∴$\widehat{BN}$=$\widehat{BM}$,
∴弧BN的长为:$\frac{60π×\frac{2\sqrt{3}}{3}}{180}$=$\frac{2\sqrt{3}}{9}$π.
故答案是$\frac{2\sqrt{3}}{9}$π.
点评 本题考查的是垂径定理,涉及到直角三角形的性质、弧长公式等知识,难度适中.求出∠MOB的度数以及⊙O的半径是解题的关键.

练习册系列答案
相关题目
14.在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形,那么下列事件是不可能事件的是( )
| A. | 这个图形既是轴对称图形又是中心对称图形 | |
| B. | 这个图形既不是轴对称图形又不是中心对称图形 | |
| C. | 这个图形是轴对称图形 | |
| D. | 这个图形是中心对称图形 |
 如图,在平面直角坐标系中,△BOC是等腰三角形,点B在x轴正半轴上,△OAD是△OBC绕点O逆时针旋转60°得到的,点A在y轴正半轴上,连接DC,线段OA的长是关于x的方程x2-4x+4=0的根
如图,在平面直角坐标系中,△BOC是等腰三角形,点B在x轴正半轴上,△OAD是△OBC绕点O逆时针旋转60°得到的,点A在y轴正半轴上,连接DC,线段OA的长是关于x的方程x2-4x+4=0的根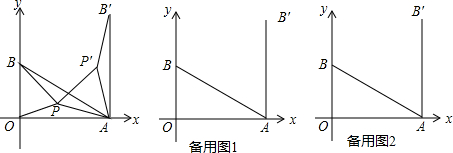
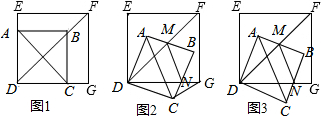
 如图,在菱形ABCD中,∠BCD=60°,BC=4,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是2$\sqrt{7}$-2.
如图,在菱形ABCD中,∠BCD=60°,BC=4,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是2$\sqrt{7}$-2.