题目内容
平面直角坐标系中,四边形ABCD与四边形A′B′C′D′关于原点O位似,点A坐标为(-2,1),它的对应点A′(1,-0.5),如果AB=2,则A′B′= .
考点:位似变换,坐标与图形性质
专题:
分析:利用位似图形的性质得出结合对应点的坐标得出位似比,即可得出答案.
解答:解:∵四边形ABCD与四边形A′B′C′D′关于原点O位似,点A坐标为(-2,1),它的对应点A′(1,-0.5),
∴两图形的位似比为:
,
∵AB=2,∴A′B′=1.
故答案为:1.
∴两图形的位似比为:
| 1 |
| 2 |
∵AB=2,∴A′B′=1.
故答案为:1.
点评:此题主要考查了位似变换,根据题意得出位似比是解题关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
二次函数y=-(x-1)2+2的顶点坐标是( )
| A、(1,-2) |
| B、(1,2) |
| C、(-1,2) |
| D、(-1,-2) |
对于实数x我们规定[x]大于x最大整数,例如[1.2]=1,[3]=3,[-2.5]=-3,[
]=6,那么x的值为( )
| x+4 |
| 10 |
| A、40 | B、45 | C、51 | D、56 |
 如图所示,D,E,F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P,Q两点,则PQ:BE=( )
如图所示,D,E,F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P,Q两点,则PQ:BE=( )| A、1:2 | B、1:4 |
| C、1:6 | D、1:8 |
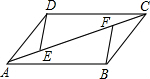 如图,AB=CD,BC=DA,E,F在AC上,且AE=CF.试说明:△BCF≌△DAE.
如图,AB=CD,BC=DA,E,F在AC上,且AE=CF.试说明:△BCF≌△DAE. 如图,在△ABC中,∠A=75°,∠B=30°,则∠ACD=
如图,在△ABC中,∠A=75°,∠B=30°,则∠ACD=