题目内容
9.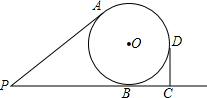 已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.
已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.
分析 连结OB、OD,如图,根据切线长定理PB=PA=4,根据切线的性质得OB⊥PC,CD⊥PC,易得四边形ODCB为矩形,则OD=BC,再利用BC=PC-PB计算出BC=2,于是得到OD=2.
解答 解: 连结OB、OD,如图,
连结OB、OD,如图,
∵线段PA、PB分别与⊙O相切于点A、B,
∴PB=PA=4,OB⊥PC,
∴∠OBC=90°,
∵CD与⊙O相切于点D,
∴∠ODC=90°,
∵CD⊥PC,
∴∠DCB=90°,
∴四边形ODCB为矩形,
∴OD=BC,
而BC=PC-PB=6-4=2,
∴OD=2,
即⊙O的半径R为2.
故答案为2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了切线长定理.

练习册系列答案
相关题目
1. 如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
 如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )
如图,在边长为(a+2)的正方形中央剪去一边长为a的小正方形,则阴影部分的面积为( )| A. | 4 | B. | 4a | C. | 4a+4 | D. | 2a+4 |
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,∠A,∠B的平分线相交于点O,则O到AB的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
19.在下列实数中,无理数是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 0 | D. | $\frac{14}{5}$ |
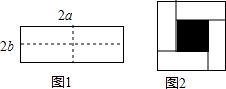 我们把如图1的一个长为2a,宽为2b的长方形,沿虚线剪成四个小长方形,再按如图2围成一个较大的正方形,则:
我们把如图1的一个长为2a,宽为2b的长方形,沿虚线剪成四个小长方形,再按如图2围成一个较大的正方形,则: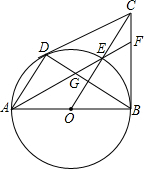 如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为△CDB的内心.其中正确的是①③(填序号).
如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为△CDB的内心.其中正确的是①③(填序号). △ABC与△DEC的位置关系如图所示,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=m,AB=n(n>m),则DF=$\frac{{n}^{2}-{m}^{2}}{m}$.
△ABC与△DEC的位置关系如图所示,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=m,AB=n(n>m),则DF=$\frac{{n}^{2}-{m}^{2}}{m}$.