题目内容
8.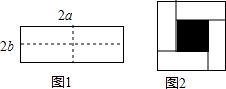 我们把如图1的一个长为2a,宽为2b的长方形,沿虚线剪成四个小长方形,再按如图2围成一个较大的正方形,则:
我们把如图1的一个长为2a,宽为2b的长方形,沿虚线剪成四个小长方形,再按如图2围成一个较大的正方形,则:(1)大正方形的边长为a+b;
(2)中间正方形(阴影部分)的边长为a-b;
(3)阴影部分的面积可表达为(a-b);也可表达为(a+b)2-4ab.
(4)比较以上两种方法,你能得到的等量关系式为(a+b)2=(a-b)2+4ab;
(5)你能借助于所得的等量关系式解决以下问题吗?试一试!
已知a-b=$\sqrt{5}$,ab=2,求(a+b)2的值.
分析 根据题意,结合图形,可以求出大正方形、中间正方形的边长,表示出阴影部分的面积,根据面积相等得到关系式,再运用关系式解决问题.
解答 解:(1)大正方形的边长为:a+b;
(2)中间正方形的边长为:a-b;
(3)阴影部分的面积为:(a-b)2,也可表达为:(a+b)2-4ab;
(4)等量关系式:(a+b)2=(a-b)2+4ab;
(5)(a+b)2=(a-b)2+4ab=5+8=13
点评 本题运用数形结合思想解决实际问题,并从中总结规律,得到相应的关系式,图形和关系式都比较简单,学生容易解答.

练习册系列答案
相关题目
16.使代数式$\frac{3}{2x-3}$有意义的x的取值范围是( )
| A. | x<$\frac{3}{2}$ | B. | x=$\frac{3}{2}$ | C. | x>$\frac{3}{2}$ | D. | x≠$\frac{3}{2}$ |
13.$\sqrt{(\sqrt{2015}-50)^{2}}$的值等于( )
| A. | ±($\sqrt{2015}$-50) | B. | $\sqrt{2015}$±50 | C. | $\sqrt{2015}$-50 | D. | 50-$\sqrt{2015}$ |

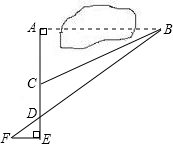 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:
数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据: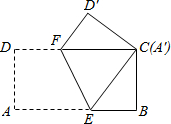 如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.
如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.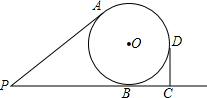 已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.
已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.