题目内容
9.已知⊙O的直径CD垂直弦AB于点E,且CE=4,DE=9,则AB的长为12.分析 根据CE=4,DE=9,可得直径CD=13,进而得出半径为6.5,从而得到OE=2.5,在直角三角形OBE中,由勾股定理得BE,然后根据垂径定理可求出AB的长.
解答 解:如图所示,
∵CE=4,DE=9,
∴CD=13,
∴OB=OC=6.5,
∴OE=2.5,
∵AB⊥CD,
∴AB=2BE,∠BEO=90°,
∴在Rt△OBE中,
由勾股定理得:BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=6,
∴AB=2BE=12.
故答案为:12.
点评 本题考查了勾股定理以及垂径定理,是基础知识要熟练掌握,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
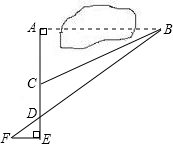 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:
数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据: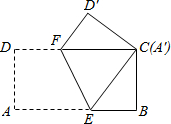 如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.
如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.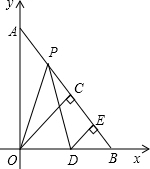 在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.
在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x. 如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.
如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.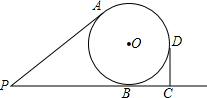 已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.
已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.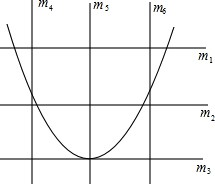 王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )