题目内容
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,∠A,∠B的平分线相交于点O,则O到AB的距离为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 如图,作辅助线;首先证明OD=OE=OF(设为λ);其次运用勾股定理求出AB的长;根据S△ABC=S△AOB+S△AOC+S△BOC,列出关于λ的方程,求出λ即可解决问题.
解答 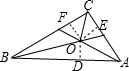 解:如图,过点O作OD⊥AB、OE⊥AC、OF⊥BC;
解:如图,过点O作OD⊥AB、OE⊥AC、OF⊥BC;
∵AO、BO分别是∠A,∠B的平分线,
∴OE=OD,OF=OD,
∴OD=OE=OF(设为λ);
∵∠C=90°,AC=3,BC=4,
∴由勾股定理得:AB=5;
由三角形的面积公式得:
$\frac{1}{2}AC•BC=\frac{1}{2}AB•λ+\frac{1}{2}AC•λ+\frac{1}{2}BC•λ$,
解得:λ=1,
故选B.
点评 该题主要考查了三角形角平分线的性质、勾股定理、三角形的面积公式等知识点及其应用问题;解题的关键是作辅助线,将△ABC分割为三个小三角形,运用三角形的面积公式列出关于λ的方程,然后求解.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
3.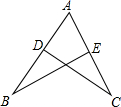 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )| A. | ∠B=∠C | B. | BE=CD | C. | BD=CE | D. | ∠ADC=∠AEB |
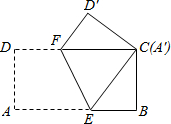 如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.
如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.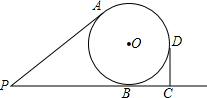 已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.
已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.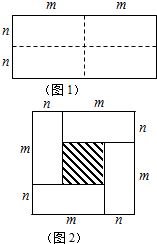 图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.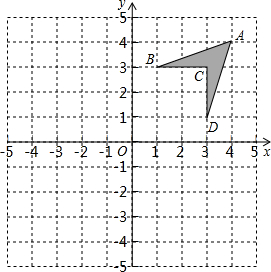 如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)
如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)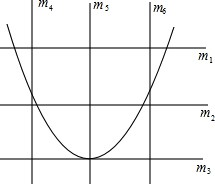 王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )