题目内容

10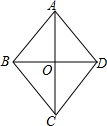．如图，在菱形ABCD中，AC与BD相交于点O，AC=8，BD=6，则菱形的边长AB等于（　　）
A．10B．$\sqrt{7}$C．6D．5

分析 根据菱形的对角线互相垂直平分求出OA、OB，再利用勾股定理列式进行计算即可得解．

解答 解：∵四边形ABCD是菱形，
∴OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AC⊥BD，
∵AC=8，BD=6，
∴OA=4，OB=3，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5，
即菱形ABCD的边长是5．
故选：D．

点评 本题主要考查了菱形的对角线互相垂直平分的性质，勾股定理的应用，熟记性质是解题的关键．

练习册系列答案
相关题目
20．已知（x+3）（x-2）=x2+ax+b，则a+b=-5．
1．已知x2-3x+1=0，求：①$x+\frac{1}{x}$的值；②${x^2}+\frac{1}{x^2}$的值．
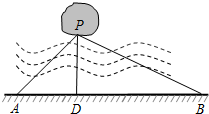18．如图，湖中有一小岛，湖边有一条笔直的观光小道AB，现决定从小岛架一座与观光小道垂直的小桥PD，在小道上测得如下数据：AB=60米，∠PAB=45°，∠PBA=30°．请求出小桥PD的长．
5．如图双曲线y1=$\frac{k}{x}$（x＞0，k＞0）与直线y2=x相交于A（1，1），点P为双曲线上一点PS∥y轴，交直线OA于S，PQ⊥y轴，SR⊥y轴，垂足分别为Q，R．
（1）求k的值，并写出y1＞y2时x的取值范围；
（2）矩形PQRS能否为正方形，若能求出P点坐标；若不能，请说明理由；
（3）在同一直角坐标系中，二次函数y3=ax2（a＞0），当x＞4-a时，y3＞y2＞y1始终成立，求a的取值范围．
15．定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．
（1）已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，求BN的长；
（2）如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC＞DE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点；
（3）已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使点C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画一种情形即可）；
（4）如图4，已知点M，N是线段AB的勾股分割点，MN＞AM≥BN，△AMC，△MND和△NBE均为等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究S△AMF，S△BEN和S四边形MNHG的数量关系，并说明理由．
2．随着互联网、移动终端的迅速发展，数字化阅读越来越普及，公交、地铁上的“低头族”越来越多．某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查（问卷调查表如图1所示）并将调查结果绘制成图2和图3所示的统计图（均不完整）．请根据统计图中提供的信息，解答下列问题：

（1）本次接受调查的总人数是5000人．
（2）请将条形统计图补充完整．
（3）在扇形统计图中，观点E的百分比是4%，表示观点B的扇形的圆心角度数为18度．
（4）假如你是该研究机构的一名成员，请根据以上调查结果，就人们如何对待数字化阅读提出你的建议．
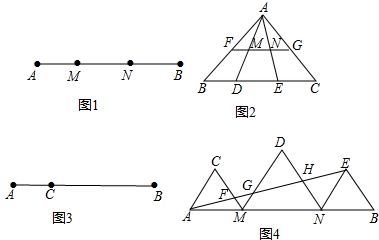
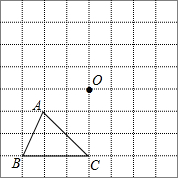19．如图，在方格网中已知格点△ABC和点O．
（1）画△A′B′C′和△ABC关于点O成中心对称；
（2）请在方格网中标出所有使以点A、O、C′、D为顶点的四边形是平行四边形的D点．
20．已知x+y=4，xy=6，求$\frac{{x}^{2}+{y}^{2}}{2}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网