题目内容
1.已知x2-3x+1=0,求:①$x+\frac{1}{x}$的值;②${x^2}+\frac{1}{x^2}$的值.分析 ①首先两边同时除以x可得x-3+$\frac{1}{x}$=0,整理可得$x+\frac{1}{x}$的值;
②直接把$x+\frac{1}{x}$两边同时平方,再展开可得${x^2}+\frac{1}{x^2}$的值.
解答 解:①∵x2-3x+1=0,
∴$\frac{{x}^{2}-3x+1}{x}$=0,
∴x-3+$\frac{1}{x}$=0,
∴$x+\frac{1}{x}$=3;
②∵$x+\frac{1}{x}$=3,
∴(x+$\frac{1}{x}$)2=9,
∴${x^2}+\frac{1}{x^2}$+2=9,
∴${x^2}+\frac{1}{x^2}$=7.
点评 此题主要考查了完全平方公式,关键是掌握完全平方公式:(a±b)2=a2±2ab+b2.可巧记为:“首平方,末平方,首末两倍中间放”.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
10.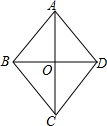 如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
 如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )| A. | 10 | B. | $\sqrt{7}$ | C. | 6 | D. | 5 |
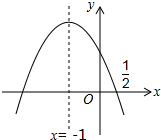 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结论是①③⑤.(填写正确结论的序号)
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点($\frac{1}{2}$,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结论是①③⑤.(填写正确结论的序号) 如图,在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24.
如图,在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24. 如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.
如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.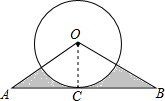 如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)
如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)