题目内容
18.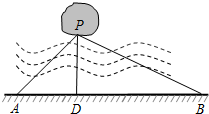 如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.
如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.
分析 设PD=x米,根据锐角三角函数的概念用x表示出AD和BD的长,根据题意列式计算即可得到答案.
解答 解:设PD=x米,
∵PD⊥AB,∴∠ADP=∠BDP=90°.
在Rt△PAD中,tan∠PAD=$\frac{x}{AD}$,
∴AD=$\frac{x}{tan45°}$=x,
在Rt△PBD中,tan∠PBD=$\frac{x}{DB}$,
∴DB=$\frac{x}{tan30°}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
又∵AB=60米,
∴x+$\sqrt{3}$x=60,
解得:x=30$\sqrt{3}$-30.
答:小桥PD的长度约为30$\sqrt{3}$-30.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念是解题的关键,解答时,把锐角三角函数的概念理解为公式,代入公式计算即可.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.下列说法正确的是( )
| A. | 随机抛一枚硬币,落地后正面一定朝上 | |
| B. | 调查重庆市民对诺贝尔文学奖获得者莫言的知晓情况用普查 | |
| C. | 在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是$\frac{1}{13}$ | |
| D. | 在一次抽奖活动中,”中奖率是$\frac{1}{100}$”表示抽奖100次就一定会中奖 |
10.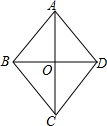 如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
 如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )| A. | 10 | B. | $\sqrt{7}$ | C. | 6 | D. | 5 |
 如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.
如图,把长方形纸片ABCD沿EF对折,若∠1=40°,则∠AEF=110°.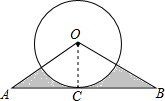 如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)
如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)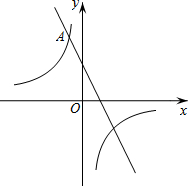 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
 如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件∠BAD=90°,使四边形ABCD是正方形(填一个即可).
如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件∠BAD=90°,使四边形ABCD是正方形(填一个即可).