题目内容
4.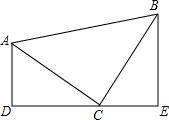 已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.
分析 由已知条件和全等三角形的判定方法可证明△ADC≌△CEB,所以可得AD=CE,BE=DE,进而可求出DE的长.
解答 解:
∵AD⊥DE于D,BE⊥DE于E,
∴∠D=∠E=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠DAC=∠BCDE,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠DAC=∠BCE}\\{∠A=∠E=90°}\\{AC=BC}\end{array}\right.$,
∴AD=CE,BE=DE,
∴DE=DC+CE=5cm.
点评 本题考查了全等三角形的性质和判定的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
16.若$\frac{1}{2}$m+1与m-2互为相反数,则m的值为( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
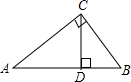 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,互余的角是∠A与∠B、∠ACD与∠BCD、∠A与∠ACD、∠B与∠BCD;互补的角是∠ADC与∠BDC、∠ADC与∠ACB、∠ACB与∠BDC.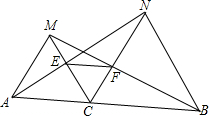 如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.
如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.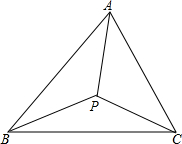 如图,P是△ABC内一点,PB=PC,∠PBA=∠PCA,求证:AP平分∠BAC.
如图,P是△ABC内一点,PB=PC,∠PBA=∠PCA,求证:AP平分∠BAC.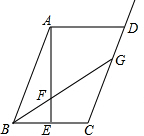 (1)探究一
(1)探究一 如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗0.8厘米,每个铁环长5厘米.设铁环间处于最大限度的拉伸状态.若要组成1.75米长的链条,则需要51个铁环.
如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗0.8厘米,每个铁环长5厘米.设铁环间处于最大限度的拉伸状态.若要组成1.75米长的链条,则需要51个铁环.