题目内容
2.已知抛物线l1的最高点为P(3,4),且经过点A(0,1),将抛物线l1绕原点O旋转180°后,得到抛物线l2,求l2的解析式.分析 由题意可知,顶点坐标为(3,4),所以可设二次函数的解析式为y=a(x-3)2+4,再将(0,1)代入,利用待定系数法即可求的解析式;根据图象绕顶点旋转180°,可得函数图象开口方向相反,顶点坐标相同,可得答案.
解答 解:设抛物线l1的解析式为:y=a(x-3)2+4,
∵点A(0,1)在抛物线l1上,
∴1=a(0-3)2+4,
∴$a=-\frac{1}{3}$,
∴抛物线l1的解析式为$y=-\frac{1}{3}{(x-3)^2}+4$,
抛物线l1绕原点O旋转180°后的顶点为(-3,-4),
所以解析式为:$y=\frac{1}{3}{(x+3)^2}-4$.
点评 本题考查了二次函数的图象与几何变换以及待定系数法求二次函数解析式,掌握旋转及平移的规律是解题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
10.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
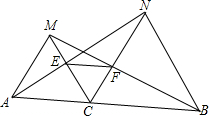 如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.
如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF. 如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗0.8厘米,每个铁环长5厘米.设铁环间处于最大限度的拉伸状态.若要组成1.75米长的链条,则需要51个铁环.
如图是由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗0.8厘米,每个铁环长5厘米.设铁环间处于最大限度的拉伸状态.若要组成1.75米长的链条,则需要51个铁环.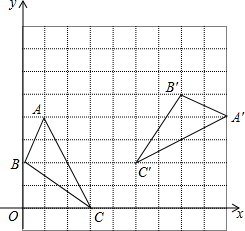 如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是(5,0).
如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是(5,0).
 在平行四边形ABCD中,要使其成为一个矩形,则应添加一个条件∠ABC=90°.
在平行四边形ABCD中,要使其成为一个矩形,则应添加一个条件∠ABC=90°.