题目内容
1.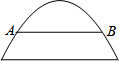 如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )| A. | 5m | B. | 6m | C. | $\sqrt{6}$m | D. | 2$\sqrt{6}$m |
分析 以拱顶为坐标原点建立平面直角坐标系,抛物线的解析式为y=ax2将A点代入抛物线方程求得a,得到抛物线解析式,再把y=-3代入抛物线解析式求得x0,进而得到答案.
解答 解:如图,以拱顶为坐标原点建立平面直角坐标系,
设抛物线方程为y=ax2,
将A(-2,-2)代入y=ax2,
解得:a=-$\frac{1}{2}$,
∴y=-$\frac{1}{2}$x2,
代入D(x0,-3)得x0=$\sqrt{6}$,
∴水面宽CD为2$\sqrt{6}$≈5,
故选A.
点评 本题主要考查二次函数的应用.建立平面直角坐标系求出函数表达式是解决问题的关键,考查了学生利用抛物线解决实际问题的能力.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.下列运算结果正确的是( )
| A. | 2a3•a4b=2a12b | B. | (a4)3=a7 | C. | (3a)3=3a3 | D. | a(a+1)=a2+a |
 如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
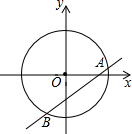 如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx-(k+1)与⊙O有两个交点A、B,则AB的最短长度是2$\sqrt{2}$.
如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx-(k+1)与⊙O有两个交点A、B,则AB的最短长度是2$\sqrt{2}$.