题目内容
13.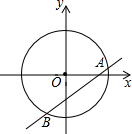 如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx-(k+1)与⊙O有两个交点A、B,则AB的最短长度是2$\sqrt{2}$.
如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx-(k+1)与⊙O有两个交点A、B,则AB的最短长度是2$\sqrt{2}$.
分析 易知直线y=kx-3k+4过定点D(1,-1),运用勾股定理可求出OD,由于过圆内定点D的所有弦中,与OD垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题
解答 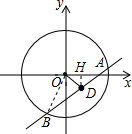 解:∵直线y=kx-(k+1)可化为y=(x-1)k-1,
解:∵直线y=kx-(k+1)可化为y=(x-1)k-1,
∴此直线恒过点(1,-1).
过点D作DH⊥x轴于点H,
∵OH=1,DH=1,OD=$\sqrt{{OH}^{2}+{DH}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
∵OB=2,
∴BD=$\sqrt{{OB}^{2}-{OD}^{2}}$=$\sqrt{{2}^{2}-{(\sqrt{2})}^{2}}$=$\sqrt{2}$,
∴AB=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查了垂径定理、勾股定理等知识,发现直线恒经过点(1,-1)以及运用“过圆内定点D的所有弦中,与OD垂直的弦最短”这个经验是解决该此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
1.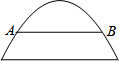 如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
 如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )
如图,有一座抛物线形拱桥,当水位线在AB位置时,拱顶(即抛物线的顶点)离水面2m,水面宽为4m,水面下降1m后,水面宽为( )| A. | 5m | B. | 6m | C. | $\sqrt{6}$m | D. | 2$\sqrt{6}$m |
18.下列各组数中,互为相反数的是( )
| A. | 2和$\frac{1}{2}$ | B. | -2和$\frac{1}{2}$ | C. | 2$\frac{3}{8}$和-2.375 | D. | +(-2)和-2 |
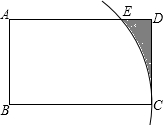 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.