题目内容
 如图所示,AD为△ABC外角∠CAE的平分线,交△ABC的外接圆于点D.求证:BD=CD.
如图所示,AD为△ABC外角∠CAE的平分线,交△ABC的外接圆于点D.求证:BD=CD.考点:圆内接四边形的性质,圆周角定理
专题:证明题
分析:利用角平分线的定义以及圆内接四边形的性质以及圆周角定理得出∠DBC=∠DCB,即可得出答案.
解答: 证明:∵AD为△ABC外角∠CAE的平分线,
证明:∵AD为△ABC外角∠CAE的平分线,
∴∠EAD=∠DAC,
∵∠EAD=∠DCB,∠DAC=∠DBC,
∴∠DBC=∠DCB,
∴DB=DC.
 证明:∵AD为△ABC外角∠CAE的平分线,
证明:∵AD为△ABC外角∠CAE的平分线,∴∠EAD=∠DAC,
∵∠EAD=∠DCB,∠DAC=∠DBC,
∴∠DBC=∠DCB,
∴DB=DC.
点评:此题主要考查了角平分线的定义以及圆内接四边形的性质以及圆周角定理等知识,得出∠DBC=∠DCB是解题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 由半圆和直角三角形组成的图形,如图,空白部分面积等于(π取3.14,精确到0.1)( )
由半圆和直角三角形组成的图形,如图,空白部分面积等于(π取3.14,精确到0.1)( )| A、15.0 | B、15.1 |
| C、15.2 | D、15.3 |
一元二次方程(3x-1)(-x+1)=3x-1的解是( )
| A、x=0 | ||
| B、x=1 | ||
C、x=
| ||
D、x=
|
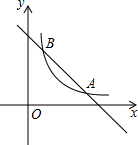 如图,直线y=-x+5与双曲线y=
如图,直线y=-x+5与双曲线y= 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P,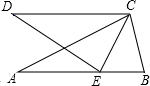 如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=
如图,把锐角△ABC绕点C顺时针旋转至△CDE处,且点E恰好落在AB上,若∠ECB=40°,则∠AED=