题目内容
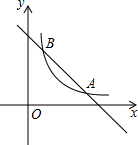 如图,直线y=-x+5与双曲线y=
如图,直线y=-x+5与双曲线y=| 4 |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:△ABC的面积最大时,点C到AB的距离最大,因此C点一定是平行于直线AB且与双曲线相切的切点.相切也就是这条直线与双曲线只有一个交点,求△ABC的最大面积,再根据判别式的意义确定平移后的直线解析式,得到平移的距离,则可根据三角形面积公式求解.
解答:解:设这条直线解析式为:y=-x+b,代入y=
得:
-x+b=
x2-bx+4=0
△=b2-16=0
b=4或-4(不合题意)
解得:x=2,y=2
故直线解析式为:y=-x+4
C点坐标为(2、2)
由解析式可知两直线与y轴交点为(0、4)(0、5)两直线与坐标轴夹角为45°,
故两直线间距离为:
,
解方程组
得
或
,
则B(4,1),A(1,4)
所以AB=
=3
,
S△ABC=
AB×h=
×3
×
=1.5
所以△ABC的最大面积=1.5.
| 4 |
| x |
-x+b=
| 4 |
| x |
x2-bx+4=0
△=b2-16=0
b=4或-4(不合题意)
解得:x=2,y=2
故直线解析式为:y=-x+4
C点坐标为(2、2)
由解析式可知两直线与y轴交点为(0、4)(0、5)两直线与坐标轴夹角为45°,
故两直线间距离为:
| ||
| 2 |
解方程组
|
|
|
则B(4,1),A(1,4)
所以AB=
| (4-1)2+(1-4)2 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
=1.5
所以△ABC的最大面积=1.5.
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
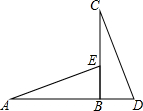 如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.
如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD. 如图所示,AD为△ABC外角∠CAE的平分线,交△ABC的外接圆于点D.求证:BD=CD.
如图所示,AD为△ABC外角∠CAE的平分线,交△ABC的外接圆于点D.求证:BD=CD.