题目内容
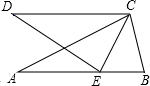如图，把锐角△ABC绕点C顺时针旋转至△CDE处，且点E恰好落在AB上，若∠ECB=40°，则∠AED=考点：旋转的性质
专题：
分析：首先证明∠CEB=∠ABC，进而求出∠CEB的度数，问题即可解决．
解答：解：由题意得：
∠DEC=∠ABC；CE=CB；
∴∠CEB=∠ABC；
∵∠ECB=40°，
∴∠CEB=∠ABC=
=70°，
∴∠AED=180°-2×70°=40°，
故答案为40°．
解：由题意得：∠DEC=∠ABC；CE=CB；
∴∠CEB=∠ABC；
∵∠ECB=40°，
∴∠CEB=∠ABC=
| 180°-40° |
| 2 |
∴∠AED=180°-2×70°=40°，
故答案为40°．
点评：该命题以三角形为载体，以旋转变换为方法，以考查全等三角形的性质为核心构造而成；灵活运用全等三角形的性质来判断、分析、证明或解答是关键．
练习册系列答案
相关题目
如图所示，AD为△ABC外角∠CAE的平分线，交△ABC的外接圆于点D．求证：BD=CD．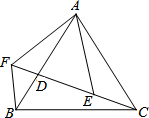
如图，已知AB=AC，AF=AE，∠EAF=∠BAC，点C、D、E、F共线．则下列结论：①△AFB≌△AEC；②BF=CE；③∠BFC=∠EAF；④AB=BC，其中错误的是