题目内容
18.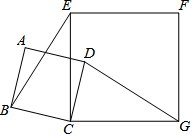 如图,在正方形ABCD和正方形ECGF中,连接BE,DG.求证:BE=DG.
如图,在正方形ABCD和正方形ECGF中,连接BE,DG.求证:BE=DG.
分析 根据正方形的性质得出BC=CD,CE=CG,∠BCD=∠ECG=90°,求出∠BCE=∠DCG,根据全等三角形的判定得出△EBC≌△GDC,根据全等三角形的性质得出即可.
解答 证明:∵在正方形ABCD和正方形ECGF中,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE=∠DCG=90°-∠ECD,
在△EBC和△GDC中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCE=∠DCG}\\{CE=CG}\end{array}\right.$
∴△EBC≌△GDC(SAS),
∴BE=DG.
点评 本题考查了正方形的性质,全等三角形的性质和判定的应用,能求出△EBC≌△GDC是解此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
20.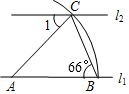 如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
 如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )
如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC,若∠ABC=66°,则∠1=( )| A. | 23° | B. | 46° | C. | 66° | D. | 48° |
13.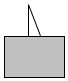 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )| A. | 一个锐角 一个钝角 | B. | 两个锐角 | ||
| C. | 一个锐角 一个直角 | D. | 一个直角 一个钝角 |
3.单项式-9x3yz2的系数与次数的和是( )
| A. | 4 | B. | -3 | C. | -5 | D. | -6 |
10.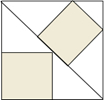 图中有三个正方形,其中构成的三角形中全等三角形的对数有( )
图中有三个正方形,其中构成的三角形中全等三角形的对数有( )
 图中有三个正方形,其中构成的三角形中全等三角形的对数有( )
图中有三个正方形,其中构成的三角形中全等三角形的对数有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
 如图,∠BAC=30°,AP平分∠BAC,GF垂直平分AP,交AC于F,Q为射线AB上一动点,若PQ的最小值为5,则AF的长10.
如图,∠BAC=30°,AP平分∠BAC,GF垂直平分AP,交AC于F,Q为射线AB上一动点,若PQ的最小值为5,则AF的长10. 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是4$\sqrt{5}$.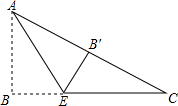 如图,在Rt△ABC中,∠B=90°,∠C=30°,EC=4,将△ABC折叠,使点B恰好在边AC上,与点B′重合,AE为折痕,则BE=2.
如图,在Rt△ABC中,∠B=90°,∠C=30°,EC=4,将△ABC折叠,使点B恰好在边AC上,与点B′重合,AE为折痕,则BE=2.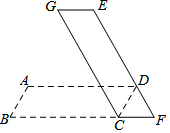 如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.
如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.