题目内容
16.一种商品,进价为每件80元.当每件按100元出售时,每月可卖出300件;已知每件商品售价每上涨2元,则该月销量会减少10件,为获得最大月利润,每件商品售价应为多少元?最大月利润是多少?分析 利用单价每每上涨2元,其月销量会减少10件,利用总利润=每件商品的利润×销量售价与月销量之间的函数关系进而利用配方法求出即可.
解答 解:设单价定为x元时,每月销售该商品的利润为y元,由题意,得
y=(x-80)[300-10×$\frac{1}{2}$(x-100)],
=-5x2+1200x-64000,
=-5(x-120)2+6000.
∴a=-5<0,抛物线的开口向下,
∴x=120时,y最大=6000.
∴单价定为120元时,每月销售该商品的利润最大,最大利润为6000.
点评 此题主要考查了二次函数的应用和二次函数最值求法等知识,熟练掌握二次函数最值求法是解题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
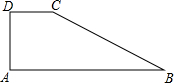 如图,四边形ABCD中,CD∥AB,AD⊥DC,DC=5,CB=15,AB=17.则四边形ABCD的面积为99.
如图,四边形ABCD中,CD∥AB,AD⊥DC,DC=5,CB=15,AB=17.则四边形ABCD的面积为99. 已知:如图,AB=CD,DA⊥CA,AC⊥BC.求证:△ADC≌△CBA.
已知:如图,AB=CD,DA⊥CA,AC⊥BC.求证:△ADC≌△CBA.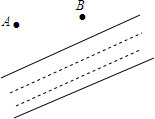 如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.
如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.