题目内容
11.等腰三角形周长为10cm,底边BC长为ycm,腰AB长为xcm,(1)写出y关于x的函数关系式;
(2)求x的取值范围.
分析 (1)等腰三角形的两个腰是相等的,根据题中条件即可列出腰长和底边长的关系式.
(2)根据2腰长的和大于底边长及底边长为正数可得自变量的取值.
解答 解:(1)∵等腰三角形的两腰相等,周长为10,
∴2x+y=10,
∴底边长y与腰长x的函数关系式为:y=-2x+10;
∵两边之和大于第三边,
∴2x>y,
∴x>2.5,
∵y>0,
∴x<5,
(2)x的取值范围是:2.5<x<5.
点评 本题主要考查对于一次函数关系式的掌握以及三角形性质的应用,判断出等腰三角形腰长的取值范围是解决本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.某校将举行一场“汉字电脑录入大赛”,要求各班推选一名同学参加比赛.为此,初三(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是95分,甲的成绩的方差是0.3,乙的成绩的方差是0.7,根据以上数据,下列说法正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
16.已知反比例函数y=$\frac{m+1}{x}$,在每一象限内,y随x的增大而减小,则m的取值范围是( )
| A. | m<0 | B. | m<-1 | C. | m>1 | D. | m>-1 |
3.能判定四边形ABCD为平行四边形的题设是( )
| A. | AB∥CD,AD=BC | B. | ∠A=∠B,∠C=∠D | C. | AB=CD,AD=BC | D. | AB=AD,CB=CD |
20.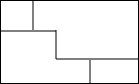 夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘的周长为280m,且桥宽忽略不计,则小桥的总长为( )
夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘的周长为280m,且桥宽忽略不计,则小桥的总长为( )
 夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘的周长为280m,且桥宽忽略不计,则小桥的总长为( )
夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘的周长为280m,且桥宽忽略不计,则小桥的总长为( )| A. | 280m | B. | 140m | C. | 90m | D. | 70m |
 如图,在平行四边形ABCD中,E为AD的中点,连接BE交AC于点F.已知△ABE的面积为4,则△ABC的面积为8.
如图,在平行四边形ABCD中,E为AD的中点,连接BE交AC于点F.已知△ABE的面积为4,则△ABC的面积为8.