题目内容
19.若等腰△ABC的一边长为a=2,另外两边长b、c恰好是关于x的一元二次方程x2-(m+3)x+m+2=0的两个根,求△ABC的周长.分析 分a=2为腰和a=2为底边两种情况分类讨论即可确定三角形的周长,注意运用三边关系进行验证.
解答 解:若a=2为腰,则b、c中还有一腰,即2是方程x2-(m+3)x+m+2=0的一个根,
∴4-2(m+3)+m+2=0,
∴m=0,
这时方程为x2-3x+2=0,
其根为1、2,
∴△ABC的周长为2+2+1=5;
若a=2为底,则b=c,即方程x2-(m+3)x+m+2=0有两个相等的实根,
∴△=0,
解得:m=-1,
这时方程为x2-2x+1=0,
∴x1=x2=1,
但1+1=2不能围成三角形,
综上可得:△ABC的周长为5.
点评 本题考查了解一元二次方程的应用:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.也考查了解等腰三角形的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16. 如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
 如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE∥BC,那么图中共有5个等腰三角形.
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE∥BC,那么图中共有5个等腰三角形. 如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
如图所示,△ABC中,AD⊥BC,AE平分∠BAC. 如图,在棱长为1米的正方体ABCD-A′B′C′D′的表面上,一只蚂蚁从顶点A爬到顶点C′的最短距离是$\sqrt{5}$米.
如图,在棱长为1米的正方体ABCD-A′B′C′D′的表面上,一只蚂蚁从顶点A爬到顶点C′的最短距离是$\sqrt{5}$米.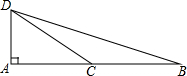 如图,点C为线段AB上一点,将线段CB绕点C旋转,得到线段CD,若DA⊥AB,AD=1,$BD=\sqrt{17}$,则BC的长为$\frac{17}{8}$.
如图,点C为线段AB上一点,将线段CB绕点C旋转,得到线段CD,若DA⊥AB,AD=1,$BD=\sqrt{17}$,则BC的长为$\frac{17}{8}$.