题目内容
20.计算:(-$\frac{{\sqrt{3}}}{3}$)-2+(π-$\sqrt{2}$)0-|$\sqrt{2}$-$\sqrt{3}}$|+tan60°+(-1)2017.分析 先依据负整数指数幂的性质、零指数幂的性质、绝对值的性质、特殊锐角三角函数值、有理数的乘方法则进行化简,最后依据实数的加减法则计算即可.
解答 解:原式=$\frac{1}{(-\frac{\sqrt{3}}{3})^{2}}$+1+$\sqrt{2}$-$\sqrt{3}$+$\sqrt{3}$-1
=3+1+$\sqrt{2}$-$\sqrt{3}$+$\sqrt{3}$-1
=3+$\sqrt{2}$.
点评 本题主要考查的是实数的运算,熟练掌握相关法则是解题的关键.

练习册系列答案
相关题目
15.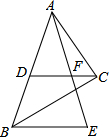 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )| A. | 6 | B. | 4 | C. | 7 | D. | 12 |
5.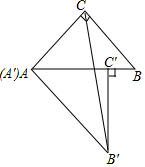 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )| A. | 3$\sqrt{3}$ | B. | 6 | C. | 3$\sqrt{2}$ | D. | $\sqrt{21}$ |
 如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).
如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3). 如图,在?ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.
如图,在?ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.
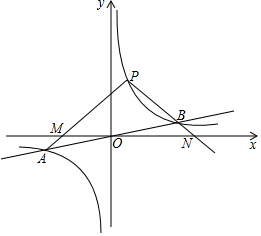 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
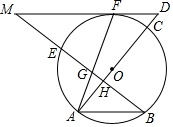 如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.
如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.