题目内容
8.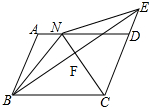 如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )
如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )| A. | 14 | B. | 11 | C. | 9 | D. | 12 |
分析 首先根据CN为∠BCE的平分线可证出ND=DC,再证明BC=CE,进而可得DN+DE=EC=8,然后再证明BN=NE可得△DNE的周长.
解答 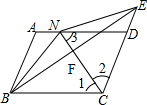 解:∵BF⊥CN,
解:∵BF⊥CN,
∴∠EFC=∠BFC=90°,
∵∠BCD的平分线CN交?ABCD的边AD于点N,
∴∠1=∠2,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴DN=DC,
在△CFE和△BCF中,$\left\{\begin{array}{l}{∠EFC=∠BFC}\\{FC=FC}\\{∠1=∠2}\end{array}\right.$,
∴△CFE≌△CFB(ASA),
∴BF=EF,BC=CE=8,
∴ND+ED=CD+ED=8,
∵BF⊥CN,
∴CN是BE的垂直平分线,
∴BN=NE=6,
∴△DNE的周长为:8+6=14,
故选:A.
点评 此题主要考查了平行四边形的性质,关键是平行四边形对边平行,CN为∠BCE的平分线可证出ND=DC.

练习册系列答案
相关题目
13.下列二次根式属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{2}{5}}$ | D. | $\sqrt{1.4}$ |
17.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是奇数 | |
| B. | 两边及其夹角对应相等的两个三角形全等 | |
| C. | 打开电视机,正在播放纪录片 | |
| D. | 三根长度为4cm,4cm,8cm的木棒能摆成三角形 |
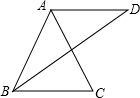 如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.
如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.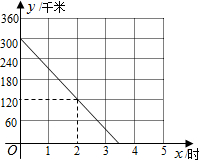 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.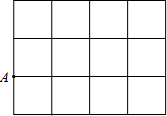 在如图所示的4×3网格中,每个小正方形的边长为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
在如图所示的4×3网格中,每个小正方形的边长为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.