题目内容
某童装加工企业为了提高工人劳动的积极性,按时完成外商订货任务,企业计划从6月份起进行工资改革.改革后工人的工资分两部分,一部分为每人每月基本工资800元.另一部分为每加工1套童装奖励若干元.若童装加工企业工人每人月平均加工150套,最不熟练的工人加工的童装套数为平均套数的60%.
(1)按6月份加工数量.如果每套童装奖励4元,最不熟练的工人的月工资为 元;按有关部门规定工人月工资的最低标准为1300元,工人加工一套童装企业至少应奖励 元(精确到0.1元);
(2)根据经营情况,企业决定每加工1套童装奖励6元,工人小张6月份工资不低于2000元,小张6月份至少加工多少套童装?
(1)按6月份加工数量.如果每套童装奖励4元,最不熟练的工人的月工资为
(2)根据经营情况,企业决定每加工1套童装奖励6元,工人小张6月份工资不低于2000元,小张6月份至少加工多少套童装?
考点:一元一次不等式的应用
专题:
分析:(1)根据工资的组成,进而得出等式和不等关系求出即可;
(2)利用企业决定每加工1套童装奖励6元,工人小张6月份工资不低于2000元,进而得出不等关系求出即可.
(2)利用企业决定每加工1套童装奖励6元,工人小张6月份工资不低于2000元,进而得出不等关系求出即可.
解答:解:(1)由题意可得出:800+4×150×60%=1160(元),
设工人加工一套童装企业应奖励y元,则:
800+y×150×60%≥1300,
解得:y≥5.6,
故答案为:1160,5.6;
(2)设小张6月份加工x套童装,根据题意得出:
800+6x≥2000,
解得:x≥200,
答:小张6月份至少加工200套童装,6月份工资不低于2000元.
设工人加工一套童装企业应奖励y元,则:
800+y×150×60%≥1300,
解得:y≥5.6,
故答案为:1160,5.6;
(2)设小张6月份加工x套童装,根据题意得出:
800+6x≥2000,
解得:x≥200,
答:小张6月份至少加工200套童装,6月份工资不低于2000元.
点评:此题主要考查了一元一次不等式的应用,根据工资组成得出不等关系是解题关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
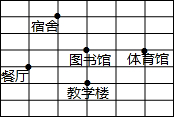 下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可).
下面是某学校的平面图,请你建立直角坐标系,描述各部门的位置(写出各点的坐标即可). 如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:
如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题: 如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2).
如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx-k的图象的交点坐标为A(m,2). 如图,已知m∥n,∠1=105°,∠2=140°,则∠α=
如图,已知m∥n,∠1=105°,∠2=140°,则∠α= 如图,在?ABCD中,已知∠B=50°,那么∠C的度数是
如图,在?ABCD中,已知∠B=50°,那么∠C的度数是