题目内容
△ABC中,AB=AC,D为BC中点,且BE⊥AC于E,交AD于P,BP=3,PE=1,求PA.
考点:角平分线的性质,全等三角形的判定与性质,勾股定理
专题:
分析:先由等腰三角形三线合一的性质得出AD⊥BC,则∠BEC=∠BDP=90°,又∠EBC=∠DBP,那么△BEC∽△BDP,根据相似三角形对应边成比例得
=
,求出BC=2
,那么BD=CD=
BC=
,由勾股定理求出PD=
=
,EC=
=2
.再证明△ADC∽△BEC,由
=
,求出AD=2
,于是利用PA=AD-PD即可求解.
| BC |
| BP |
| BE |
| BD |
| 6 |
| 1 |
| 2 |
| 6 |
| BP2-BD2 |
| 3 |
| BC2-BE2 |
| 2 |
| AD |
| BE |
| DC |
| EC |
| 3 |
解答: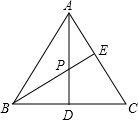 解:∵AB=AC,D为BC的中点,
解:∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵BE⊥AC,
∴∠BEC=∠BDP=90°,
又∵∠EBC=∠DBP,
∴△BEC∽△BDP,
∴
=
,即
=
,
∴BC=2
,
∴BD=CD=
BC=
,
∴PD=
=
=
,
EC=
=
=2
.
在△ADC与△BEC中,
∵∠C=∠C,∠ADC=∠BEC=90°,
∴△ADC∽△BEC,
∴
=
,即
=
,
解得AD=2
,
∴PA=AD-PD=2
-
=
.
 解:∵AB=AC,D为BC的中点,
解:∵AB=AC,D为BC的中点,∴AD⊥BC,
∵BE⊥AC,
∴∠BEC=∠BDP=90°,
又∵∠EBC=∠DBP,
∴△BEC∽△BDP,
∴
| BC |
| BP |
| BE |
| BD |
| BC |
| 3 |
| 4 | ||
|
∴BC=2
| 6 |
∴BD=CD=
| 1 |
| 2 |
| 6 |
∴PD=
| BP2-BD2 |
32-(
|
| 3 |
EC=
| BC2-BE2 |
(2
|
| 2 |
在△ADC与△BEC中,
∵∠C=∠C,∠ADC=∠BEC=90°,
∴△ADC∽△BEC,
∴
| AD |
| BE |
| DC |
| EC |
| AD |
| 4 |
| ||
2
|
解得AD=2
| 3 |
∴PA=AD-PD=2
| 3 |
| 3 |
| 3 |
点评:本题考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理,求出PD与AD的长是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

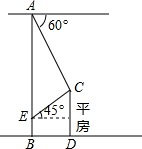 如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为
如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为 如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.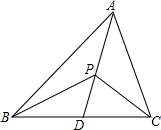 如图,在△ABC中,AB>AC>BC,P为三角形内任意一点,连接AP,并延长交BC于D.求证:
如图,在△ABC中,AB>AC>BC,P为三角形内任意一点,连接AP,并延长交BC于D.求证: