题目内容
函数y=-（x+1）2+4的图象绕着点（1，0）顺时针旋转90°后的图象对应的解析式为 ．
考点：二次函数图象与几何变换
专题：
分析：根据旋转前后的图形全等，可得a、h、k不变，根据顺时针旋转90°，可得顶点式解析式．
解答：解：函数y=-（x+1）2+4的图象绕着点（1，0）顺时针旋转90°后的图象对应的解析式为 x=-（y-1）2+4，
故答案为：x=-（y-1）2+4．
故答案为：x=-（y-1）2+4．
点评：本题考查了二次函数图象与几何变换：由于抛物线旋转后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
如图，在矩形ABCD中，点E在AB边上，点F在AD边上，且AE=DF，AF=CD，连接线段CE、EF、CF．点G是线段CE的中点，点M是线段EF上一点，过点G作GN⊥GM，将CF于点N．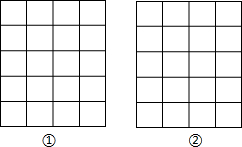
如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：
如图，MC∥AB，NC∥AB，则点M，C，N在同一条直线上，理由是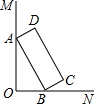
如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，AB=4，BC=1．当点B在边ON上运动时，点A随之在边OM上运动，运动过程中矩形ABCD的形状保持不变，则点D到点O的最大距离是