题目内容
3.化简:$\frac{1}{2+1}$+$\frac{1}{\sqrt{7}+2}$+$\frac{1}{\sqrt{10}+\sqrt{7}}$+…+$\frac{1}{\sqrt{3n+1}+\sqrt{3n-2}}$.分析 首先把分母有理化,提取公因式,进一步抵消计算得出答案即可.
解答 解:原式=$\frac{1}{3}$×(2-1)+$\frac{1}{3}$($\sqrt{7}$-2)+$\frac{1}{3}$($\sqrt{10}$-$\sqrt{7}$)+…+$\frac{1}{3}$($\sqrt{3n+1}$-$\sqrt{3n-2}$)
=$\frac{1}{3}$×(2-1+$\sqrt{7}$-2+$\sqrt{10}$-$\sqrt{7}$+…+$\sqrt{3n+1}$-$\sqrt{3n-2}$)
=$\frac{1}{3}$($\sqrt{3n+1}$-1).
点评 此题考查二次根式的混合运算,掌握分母有理化的方法是解决问题的关键.

练习册系列答案
相关题目
 已知函数y=ax2+bx+c的图象如图所示:则△>0;a>0;b<0;c<0;a+b+c<0;a-b+c>0.
已知函数y=ax2+bx+c的图象如图所示:则△>0;a>0;b<0;c<0;a+b+c<0;a-b+c>0.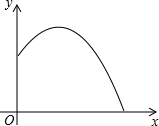 如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )
如图是某运动员打羽毛球的抛物线示意图,已知打出羽毛球的高度y(m)与水平距离x(m)之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7,则该羽毛球落地时距离发出点( )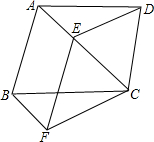 如图,四边形ABCD的AB边平行于CD边,在对角线上取一点E,使∠DEC=∠ABC,若CE:CD=CD:CA.
如图,四边形ABCD的AB边平行于CD边,在对角线上取一点E,使∠DEC=∠ABC,若CE:CD=CD:CA.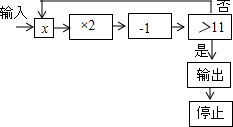 如图为某一运算程序,规定:程序运行到判断“结果是否大于11”为一次运算,若输入整数x后,运算进行了2次就输出停止,则满足条件的整数x是4、5或6.
如图为某一运算程序,规定:程序运行到判断“结果是否大于11”为一次运算,若输入整数x后,运算进行了2次就输出停止,则满足条件的整数x是4、5或6. 如图是反比例函数y=$\frac{k}{x}$的图象,那么k与0的大小关系是k>0.
如图是反比例函数y=$\frac{k}{x}$的图象,那么k与0的大小关系是k>0.