题目内容
17. 已知函数y=ax2+bx+c的图象如图所示:则△>0;a>0;b<0;c<0;a+b+c<0;a-b+c>0.
已知函数y=ax2+bx+c的图象如图所示:则△>0;a>0;b<0;c<0;a+b+c<0;a-b+c>0.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答  解:如图所示,抛物线与x轴有2个交点,则△>0.
解:如图所示,抛物线与x轴有2个交点,则△>0.
抛物线开口方向向上,则a>0.
对称轴在y轴的右侧,则a、b异号,即b<0.
抛物线与y轴交于负半轴,则c<0.
当x=1时,y<0,即a+b+c<0.
当x=-1时,y>0,即a+b+c>0.
故答案是:>;>;<;<;<;>.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
8. 如图,下面几何图形的俯视图是( )
如图,下面几何图形的俯视图是( )
 如图,下面几何图形的俯视图是( )
如图,下面几何图形的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5. 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,则下列选项中的弧属于优弧的是( )| A. | $\widehat{AC}$ | B. | $\widehat{AD}$ | C. | $\widehat{ACD}$ | D. | $\widehat{ADB}$ |
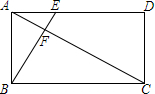 如图,在矩形ABCD中,AB=4cm,AD=8cm,点E在边AD上,AE:ED=1:3,AC、BE交于点F.
如图,在矩形ABCD中,AB=4cm,AD=8cm,点E在边AD上,AE:ED=1:3,AC、BE交于点F. 如图,平行四边形ABCD中,E是边BC的中点,AE交BD于点F,如果BF=4,那么FD=8.
如图,平行四边形ABCD中,E是边BC的中点,AE交BD于点F,如果BF=4,那么FD=8.